TOPICS
Search

Harmonic Number

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
HarmonicNumber

A harmonic number is a number of the form

H_n=sum_(k=1)^n1/k
(1)

arising from truncation of the harmonic series. A harmonic number can be expressed analytically as

H_n=gamma+psi_0(n+1),
(2)

where gamma is the Euler-Mascheroni constant and Psi(x)=psi_0(x) is the digamma function.

The first few harmonic numbers H_n are 1, 3/2, 11/6, 25/12, 137/60, ... (OEIS A001008 and A002805). The numbers of digits in the numerator of H_(10^n) for n=0, 1, ... are 1, 4, 41, 434, 4346, 43451, 434111, 4342303, 43428680, ... (OEIS A114467), with the corresponding number of digits in the denominator given by 1, 4, 40, 433, 4345, 43450, 434110, 4342302, 43428678, ... (OEIS A114468). These digits converge to what appears to be the decimal digits of log_(10)e=0.43429448... (OEIS A002285).

HarmonicNumberPrimes

The first few indices n such that the numerator of H_n is prime are given by 2, 3, 5, 8, 9, 21, 26, 41, 56, 62, 69, ... (OEIS A056903). The search for prime numerators has been completed up to 81780 by E. W. Weisstein (May 13, 2009), and the following table summarizes the largest known values.

ndecimal digitsdiscoverer
6394227795E. W. Weisstein (Feb. 14, 2007)
6929430067E. W. Weisstein (Feb. 1, 2008)
6992730301E. W. Weisstein (Mar. 11, 2008)
7744933616E. W. Weisstein (Apr. 4, 2009)
7812833928E. W. Weisstein (Apr. 9, 2009)
7899334296E. W. Weisstein (Apr. 17, 2009)
8165835479E. W. Weisstein (May. 12, 2009)

The denominators of H_n appear never to be prime except for the case H_2=3/2. Furthermore, the denominator is never a prime power (except for this case) since the denominator is always divisible by the largest power of 2 less than or equal to n, and also by any prime p with n/2<p<=n.

The harmonic numbers are implemented as HarmonicNumber[n].

The values of n such that H_n equals or exceeds 1, 2, 3, ... are given by 1, 4, 11, 31, 83, 227, 616, 1674, ... (OEIS A004080). Another interesting sequence is the number of terms in the simple continued fraction of H_(10^n) for n=0, 1, 2, ..., given by 1, 8, 68, 834, 8356, 84548, 841817, 8425934, 84277586, ... (OEIS A091590), which is conjectured to approach 12ln2/pi^2=0.8427659... (OEIS A089729).

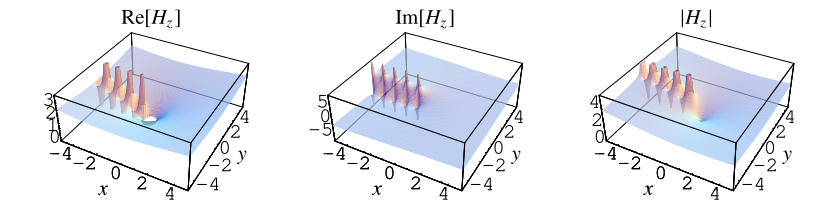
HarmonicNumberReIm
HarmonicNumberContours

The definition of harmonic numbers can also be extended to the complex plane, as illustrated above.

Based on their definition, harmonic numbers satisfy the obvious recurrence equation

H_n=1/n+H_(n-1)
(3)

with H_1=1.

The number formed by taking alternate signs in the sum also has an explicit analytic form

H_n^'=sum_(k=1)^(n)((-1)^(k+1))/k
(4)
=ln2+1/2(-1)^n[psi_0(1/2n+1/2)-psi_0(1/2n+1)]
(5)
=ln2+1/2(-1)^n[H_((n-1)/2)-H_(n/2)].
(6)

H_(2n)^' has the particularly beautiful form

H_(2n)^'=sum_(k=1)^(2n)((-1)^(k+1))/k
(7)
=sum_(k=1,3,...)^(2n)((-1)^(k+1))/k+sum_(k=2,4,...)^(2n)((-1)^(k+1))/k
(8)
=sum_(k=1,3,...)^(2n)1/k-sum_(k=2,4,...)^(2n)1/k
(9)
=(sum_(k=1,3,...)^(2n)1/k+sum_(k=2,4,...)^(2n)1/k)-2sum_(k=2,4,...)^(2n)1/k
(10)
=sum_(k=1)^(2n)1/k-sum_(k=1)^(n)1/k
(11)
=H_(2n)-H_n.
(12)

The harmonic number H_n is never an integer except for H_1, which can be proved by using the strong triangle inequality to show that the 2-adic value of H_n is greater than 1 for n>1. This result was proved in 1915 by Taeisinger, and the more general results that any number of consecutive terms not necessarily starting with 1 never sum to an integer was proved by Kűrschák in 1918 (Hoffman 1998, p. 157).

The harmonic numbers have odd numerators and even denominators. The nth harmonic number is given asymptotically by

H_n∼lnn+gamma+1/(2n)-1/(12)n^(-2)+1/(120)n^(-4)-1/(252)n^(-6)+...,
(13)

where gamma is the Euler-Mascheroni constant (Conway and Guy 1996; Havil 2003, pp. 79 and 89), where the general (2n)th term is zeta(1-2n), giving -12, 120, -252, 240, ... for n=1, 2, ... (OEIS A006953). This formula is a special case of an Euler-Maclaurin integration formulas (Havil 2003, p. 79).

HarmonicNumberInequalities

Inequalities bounding H_n include

1/(2(n+1))<H_n-lnn-gamma<1/(2n)
(14)

(Young 1991; Havil 2003, pp. 73-75) and

1/(24(n+1)^2)<H_n-ln(n+1/2)-gamma<1/(24n^2)
(15)

(DeTemple 1991; Havil 2003, pp. 76-78).

An interesting analytic sum is given by

sum_(n=1)^infty(H_n)/(n·2^n)=1/(12)pi^2.
(16)

(Coffman 1987). Borwein and Borwein (1995) show that

sum_(n=1)^(infty)(H_n^2)/((n+1)^2)=(11)/4zeta(4)=(11)/(360)pi^4
(17)
sum_(n=1)^(infty)(H_n^2)/(n^2)=(17)/4zeta(4)=(17)/(360)pi^4
(18)
sum_(n=1)^(infty)(H_n)/(n^3)=5/4zeta(4)=1/(72)pi^4
(19)
sum_(n=1)^(infty)(H_n)/(n^4)=3zeta(5)-1/6pi^2zeta(3)
(20)
sum_(n=1)^(infty)(H_n)/(n^5)=1/(540)pi^6-1/2[zeta(3)]^2,
(21)

where zeta(z) is the Riemann zeta function. The first of these had been previously derived by de Doelder (1991), and the third by Goldbach in a 1742 letter to Euler (Borwein and Bailey 2003, pp. 99-100; Bailey et al. 2007, p. 256). These identities are corollaries of the identity

1/piint_0^pix^2{ln[2cos(1/2x)]}^2dx=(11)/2zeta(4)=(11)/(180)pi^4
(22)

(Borwein and Borwein 1995). Additional identities due to Euler are

sum_(n=1)^(infty)(H_n)/(n^2)=2zeta(3)
(23)
2sum_(n=1)^(infty)(H_n)/(n^m)=(m+2)zeta(m+1)-sum_(n=1)^(m-2)zeta(m-n)zeta(n+1)
(24)

for m=2, 3, ... (Borwein and Borwein 1995), where zeta(3) is Apéry's constant. These sums are related to so-called Euler sums.

A general identity due to B. Cloitre (pers. comm., Jan. 7, 2006) is

sum_(k=1)^infty(H_k)/((k+1)_m)=1/((m-1)!(m-1)^2),
(25)

where (x)_n is a Pochhammer symbol.

Gosper gave the interesting identity

sum_(i=0)^(infty)(z^iH_i)/(i!)=-e^zsum_(k=1)^(infty)((-z)^k)/(kk!)
(26)
=e^z[lnz+Gamma(0,z)+gamma],
(27)

where Gamma(0,z) is the incomplete gamma function and gamma is the Euler-Mascheroni constant.

G. Huvent (2002) found the beautiful formula

zeta(5)=-(16)/(11)sum_(n=1)^infty([2(-1)^n+1]h_n)/(n^4).
(28)

A beautiful double series is given by

sum_(k=1)^inftysum_(j=1)^infty(H_j(H_(k+1)-1))/(kj(k+1)(j+k)) =-4zeta(2)-2zeta(3)+4zeta(2)zeta(3)+2zeta(5)
(29)

(Bailey et al. 2007, pp. 273-274). Another double sum is

sum_(i=0)^(k-1)sum_(j=k)^n((-1)^(i+j-1))/(j-i)(n; i)(n; j)=sum_(i=1)^(k-1)(n; i)^2(H_(n-i)-H_i)
(30)

for 1<=k<=n (Sondow 2003, 2005).

There is an unexpected connection between the harmonic numbers and the Riemann hypothesis.

Generalized harmonic numbers in power r can be defined by the relationship

H_(n,r)=sum_(k=1)^n1/(k^r),
(31)

where

H_(n,1)=H_n.
(32)

These number are implemented as HarmonicNumber[n, r].

The numerators of the special case H_(n,2) are known as Wolstenholme numbers. B. Cloitre (pers. comm., ) gave the surprising identity

H_(n,2)=1/2sum_(i=1)^nsum_(j=1)^n((i-1)!(j-1)!)/((i+j)!)+3/2sum_(k=1)^n1/(k^2(2k; k))
(33)

which relates H_(n,2) to an indefinite version of a famous series for zeta(2). H_(n,2) also satisfies

lim_(n->infty)H_(n,2)=zeta(2)=(pi^2)/6,
(34)

where zeta(2) is the Riemann zeta function. This follows from the identity

H_(n,2)=zeta(2)-gamma_1(n+1),
(35)

where gamma_1(z) is the trigamma function since

lim_(n->infty)gamma_1(n+1)=0.
(36)

For odd r>=3, the generalized harmonic numbers have the explicit form

H_(n,r)=n^(-r)+(psi_(r-1)(n))/(Gamma(r))+zeta(r),
(37)

where psi_r(n) is the polygamma function, Gamma(r) is the gamma function, and zeta(r) is the Riemann zeta function.

The 2-index harmonic numbers satisfy the identity

H_(n,r)=2^(r-1)(H_(2n,r)-H_(2n,r)^')
(38)

(P. Simon, pers. comm., Aug. 30, 2004).

Sums of the generalized harmonic numbers H_(n,r) include

sum_(n=1)^inftyH_(n,r)z^n=(Li_r(z))/(1-z)
(39)

for |z|<1, where Li_r(z) is a polylogarithm,

sum_(k=1)^(infty)(H_(k,1))/(k(z+1)^k)=-Li_2(-1/z)
(40)
sum_(k=1)^(infty)(H_(k,1))/(kphi^(2k))=1/(15)pi^2-1/2[csch^(-1)2]^2
(41)
sum_(k=1)^(infty)(H_(k,1))/(k^22^k)=zeta(3)-1/(12)pi^2ln2
(42)
sum_(k=1)^(infty)(H_(k,2))/(k^4)=[zeta(3)]^2-(pi^6)/(2835)
(43)
sum_(k=1)^(infty)(H_(k,2))/(k2^k)=5/8zeta(3)
(44)
sum_(k=1)^(infty)(H_(k,4))/(k^2)=(37pi^6)/(11340)-[zeta(3)]^2,
(45)

where equations (40), (41), (42), and (44) are due to B. Cloitre (pers. comm., Oct. 4, 2004) and Li_2(z) is a dilogarithm. In general,

sum_(k=1)^infty(H_(k,r))/(k^r)=1/2{[zeta(r)]^2+zeta(2r)}
(46)

(P. Simone, pers. comm. June 2, 2003). The power harmonic numbers also obey the unexpected identity

9H_(8,n)-19H_(9,n)+10H_(10,n)+sum_(k=1)^(n-1)[H_(8,n-k)H_(9,k)-H_(9,n-k)H_(9,k) -H_(8,n-k)H_(10,k)+H_(9,n-k)H_(10,k)]=0
(47)

(M. Trott, pers. comm.).

P. Simone (pers. comm., Aug. 30, 2004) showed that

[C(t)]^2+[S(t)]^2=1/(90)pi^4+2/3pi^2C(t) -2sum_(m=1)^infty((H_(m,2))/(m^2)+(2H_m)/(m^3))cos(mt),
(48)

where

C(t)=sum_(n=1)^(infty)(cos(nt))/(n^2)
(49)
=1/2[Li_2(e^(-it))+Li_2(e^(it))]
(50)
S(t)=sum_(n=1)^(infty)(sin(nt))/(n^2)
(51)
=1/2i[Li_2(e^(-it))-Li_2(e^(it))].
(52)

This gives the special results

sum_(n=1)^infty(H_n)/(n^3)=1/(72)pi^4 1/8sum_(n=1)^infty((2H_(4k,2))/(k^2)+(H_(2k))/(k^3))=(211pi^4)/(11520)-K^2 2sum_(k=1)^infty[((-1)^(k+1)H_(k,2))/(k^2)+(2(-1)^(k+1)H_k)/(k^3)]=(37pi^4)/(720)
(53)

for t=0,pi/2,pi, respectively.

Conway and Guy (1996) define the second-order harmonic number by

H_n^((2))=sum_(i=1)^(n)H_i
(54)
=(n+1)(H_(n+1)-1)
(55)
=(n+1)(H_(n+1)-H_1),
(56)

the third-order harmonic number by

H_n^((3))=sum_(i=1)^nH_i^((2))=(n+2; 2)(H_(n+2)-H_2),
(57)

and the kth-order harmonic number by

H_n^((k))=(n+k-1; k-1)(H_(n+k-1)-H_(k-1)).
(58)

A slightly different definition of a two-index harmonic number c_n^((j)) is given by Roman (1992) in connection with the harmonic logarithm. Roman (1992) defines this by

c_n^((0))={1 for n>=0; 0 for n<0
(59)
c_0^((j))={1 for j=0; 0 for j!=0
(60)

plus the recurrence relation

c_n^((j))=c_n^((j-1))+nc_(n-1)^((j)).
(61)

For general n>0 and j>0, this is equivalent to

c_n^((j))=sum_(i=1)^n1/ic_i^((j-1)),
(62)

and for n>0, it simplifies to

c_n^((j))=sum_(i=1)^n(n; i)(-1)^(i-1)i^(-j).
(63)

For n<0, the harmonic number can be written

c_n^((j))=(-1)^j|_n]!s(-n,j),
(64)

where |_n]! is the Roman factorial and s is a Stirling number of the first kind.

A separate type of number sometimes also called a "harmonic number" is a harmonic divisor number (or Ore number).

See also

Apéry's Constant, Book Stacking Problem, Egyptian Fraction, Euler Sum, Faulhaber's Formula, Harmonic Divisor Number, Harmonic Logarithm, Harmonic Series, Unit Fraction, Wolstenholme Number

Related Wolfram sites

http://functions.wolfram.com/GammaBetaErf/HarmonicNumber/, http://functions.wolfram.com/GammaBetaErf/HarmonicNumber2/

Portions of this entry contributed by Jonathan Sondow (author's link)

Explore with Wolfram|Alpha

References

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.Borwein, D. and Borwein, J. M. "On an Intriguing Integral and Some Series Related to zeta(4)." Proc. Amer. Math. Soc. 123, 1191-1198, 1995.Coffman, S. W. "Problem 1240 and Solution: An Infinite Series with Harmonic Numbers." Math. Mag. 60, pp. 118-119, 1987.Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 143 and 258-259, 1996.de Doelder, P. J. "On Some Series Containing Psi(x)-Psi(y) and (Psi(x)-Psi(y))^2 for Certain Values of x and y." J. Comp. Appl. Math. 37, 125-141, 1991.DeTemple, D. W. "The Non-Integer Property of Sums of Reciprocals of Consecutive Integers." Math. Gaz. 75, 193-194, 1991.Flajolet, P. and Salvy, B. "Euler Sums and Contour Integral Representation." Experim. Math. 7, 15-35, 1998.Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Harmonic Numbers" and "Harmonic Summation." §6.3 and 6.4 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 272-282, 1994.Gosper, R. W. "harmonic Summation and exponential gfs." math-fun@cs.arizona.edu posting, Aug. 2, 1996.Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.Huvent, G. "Autour de la primitive de t^pcoth(alphat/2)." Feb. 3, 2002. http://perso.orange.fr/gery.huvent/articlespdf/Autour_primitive.pdf.Roman, S. "The Logarithmic Binomial Formula." Amer. Math. Monthly 99, 641-648, 1992.Roman, S. The Umbral Calculus. New York: Academic Press, p. 99, 1984.Savio, D. Y.; Lamagna, E. A.; and Liu, S.-M. "Summation of Harmonic Numbers." In Computers and Mathematics (Ed. E. Kaltofen and S. M. Watt). New York: Springer-Verlag, pp. 12-20, 1989.Sloane, N. J. A. Sequences A001008/M2885, A002285/M3210, A002805/M1589, A004080, A006953/M2039, A056903, A082912, A089729, A091590, A096618, A114467, and A114468 in "The On-Line Encyclopedia of Integer Sequences."Sondow, J. "Criteria for Irrationality of Euler's Constant." Proc. Amer. Math. Soc. 131, 3335-3344, 2003.Sondow, J. "Problem 11026: An Identity Involving Harmonic Numbers." Amer. Math. Monthly 112, 367-369, 2005.Trott, M. "The Mathematica Guidebooks Additional Material: Harmonic Numbers Inversion." http://www.mathematicaguidebooks.org/additions.shtml#S_3_06.Young, R. M. "Euler's Constant." Math. Gaz. 75, 187-190, 1991.

Referenced on Wolfram|Alpha

Harmonic Number

Cite this as:

Sondow, Jonathan and Weisstein, Eric W. "Harmonic Number." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/HarmonicNumber.html

Subject classifications