The most general form of "an" exponential function is a power-law function of the form
(1)
where exponentially
increasing function and when exponentially
decreasing function .
In contrast, "the" exponential function (in elementary contexts sometimes called the "natural exponential function ")
is the function defined by
(2)
where e natural
logarithm . The function differential
equation derivative , so
(3)
The exponential function entire function in
the complex plane .
The exponential function is implemented in the Wolfram
Language as Exp z ].
The "natural" and general exponential functions are related to one another by a simple scalings of the variable
(4)
where natural logarithm .
The exponential function has the simple Maclaurin
series
(5)
where factorial , and satisfies the limit
(6)
The exponential function satisfies the identity
(7)
It is also related to trigonometric functions via the identities
where Gudermannian (Beyer 1987, p. 164; Zwillinger
1995, p. 485).
If
(12)
Similarly, if
(13)
then
The exponential function has continued fraction
(17)
(Wall 1948, p. 348).
The above plot shows the function
Integrals involving the exponential function include
(Borwein et al. 2004, p. 55).
See also Cis ,
Complex Exponentiation ,
e ,
Euler
Formula ,
Exponent ,
Exponent
Laws ,
Exponential Decay ,
Exponential
Growth ,
Exponential Ramp ,
Exponentially
Decreasing Function ,
Exponentially
Increasing Function ,
Fourier
Transform--Exponential Function ,
Gudermannian ,
Natural Exponential Function ,
Phasor ,
Power ,
Sigmoid Function Explore this
topic in the MathWorld classroom
Related Wolfram sites http://functions.wolfram.com/ElementaryFunctions/Exp/
Explore with Wolfram|Alpha
References Abramowitz, M. and Stegun, I. A. (Eds.). "Exponential Function." §4.2 in Handbook
of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. Beyer, W. H. CRC
Standard Mathematical Tables, 28th ed. Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation
in Mathematics: Computational Paths to Discovery. Finch, S. "Linear Independence of Exponential Functions."
http://algo.inria.fr/csolve/sstein.html . Fischer,
G. (Ed.). Plates 127-128 in Mathematische
Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Krantz, S. G. "The
Exponential and Applications." §1.2 in Handbook
of Complex Variables. Spanier,
J. and Oldham, K. B. "The Exponential Function An
Atlas of Functions. Trott,
M. "Elementary Transcendental Functions." §2.2.3 in The
Mathematica GuideBook for Programming. http://www.mathematicaguidebooks.org/ . Wall,
H. S. Analytic
Theory of Continued Fractions. Yates,
R. C. "Exponential Curves." A
Handbook on Curves and Their Properties. Zwillinger, D. (Ed.). CRC
Standard Mathematical Tables and Formulae. Referenced
on Wolfram|Alpha Exponential Function
Cite this as:
Weisstein, Eric W. "Exponential Function."
From MathWorld https://mathworld.wolfram.com/ExponentialFunction.html
Subject classifications
,
,
and
are real numbers,
is a positive real number, and
is a real variable. When
is positive,
is an exponentially
increasing function and when
is negative,
is an exponentially
decreasing function.
is the base of the natural
logarithm. The function
is also the unique solution of the differential
equation
with initial condition
. In other words, the exponential function is its own
derivative, so
defined for complex variable
is an entire function in
the complex plane.
and multiplicative prefactors via the identity
is the natural logarithm.
is a factorial, and satisfies the limit
is the Gudermannian (Beyer 1987, p. 164; Zwillinger
1995, p. 485).
,

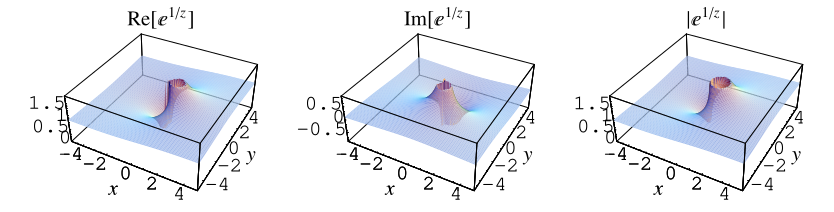
(Trott 2004, pp. 165-166).