A complex number may be taken to the power of another complex number. In particular, complex exponentiation satisfies
|
(1)
|
where
is the complex argument. Written explicitly in
terms of real and imaginary parts,
![(a+bi)^(c+di)=(a^2+b^2)^(c/2)e^(-darg(a+ib))×{cos[carg(a+ib)+1/2dln(a^2+b^2)]+isin[carg(a+ib)+1/2dln(a^2+b^2)]}.](/images/equations/ComplexExponentiation/NumberedEquation2.svg) |
(2)
|
An explicit example of complex exponentiation is given by
![(1+i)^(1+i)=sqrt(2)e^(-pi/4)[cos(1/4pi+1/2ln2)+isin(1/4pi+1/2ln2)].](/images/equations/ComplexExponentiation/NumberedEquation3.svg) |
(3)
|
A complex number taken to a complex number can be real. In fact, the famous example
|
(4)
|
shows that the power of the purely imaginary to itself is real.
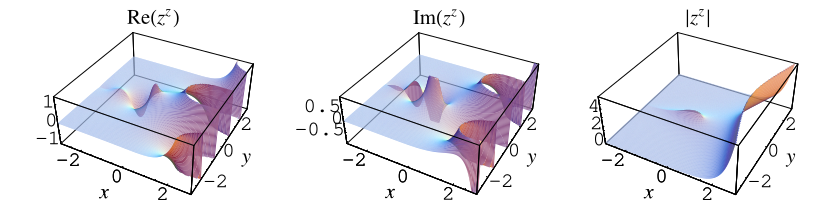
In fact, there is a family of values such that
is real, as can be seen by writing
|
(5)
|
This will be real when , i.e., for
|
(6)
|
for
an integer. For positive
, this gives roots
or
|
(7)
|
where
is the Lambert W-function. For
, this simplifies to
|
(8)
|
For ,
2, ..., these give the numeric values 1, 2.92606 (OEIS A088928),
4.30453, 5.51798, 6.63865, 7.6969, ....