Factorial

The factorial is defined for a positive integer as

(1)

So, for example, . An older notation for the factorial was written (Mellin 1909; Lewin 1958, p. 19; Dudeney 1970; Gardner 1978; Conway and Guy 1996).

The special case is defined to have value , consistent with the combinatorial interpretation of there being exactly one way to arrange zero objects (i.e., there is a single permutation of zero elements, namely the empty set ).

The factorial is implemented in the Wolfram Language as Factorial[n] or n!.

The triangular number can be regarded as the additive analog of the factorial . Another relationship between factorials and triangular numbers is given by the identity

(2)

(K. MacMillan, pers. comm., Jan. 21, 2008).

The factorial gives the number of ways in which objects can be permuted. For example, , since the six possible permutations of are , , , , , . The first few factorials for , 1, 2, ... are 1, 1, 2, 6, 24, 120, ... (OEIS A000142).

The numbers of digits in for , 1, ... are 1, 7, 158, 2568, 35660, 456574, 5565709, 65657060, ... (OEIS A061010).

Generalizations of the factorial such as the double factorial and multifactorial can be defined. Note, however, that these are not equal to nested factorials , , etc.

The first few values of for , 2, ... are 1, 2, 720, 620448401733239439360000, ... (Eureka 1974; OEIS A000197). The numbers of digits in are 1, 1, 3, 24, 199, 1747, ... (OEIS A063979).

As grows large, factorials begin acquiring tails of trailing zeros. To calculate the number of trailing zeros for , use

(3)

where

(4)

and is the floor function (Gardner 1978, p. 63; Ogilvy and Anderson 1988, pp. 112-114). For , 2, ..., the number of trailing zeros are 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, ... (OEIS A027868). This is a special application of the general result first discovered by Legendre in 1808 that the largest power of a prime dividing is

(5)

(Landau 1974, pp. 75-76; Honsberger 1976; Hardy and Wright 1979, pp. 342; Ribenboim 1989; Ingham 1990, p. 20; Graham et al. 1994; Vardi 1991; Hardy 1999, pp. 18 and 21; Havil 2003, p. 165; Boros and Moll 2004, p. 5). This can be implemented in the Wolfram Language as

  HighestPower[p_?PrimeQ, n_] :=
    Sum[Floor[n/p^k], {k, Floor[Log[p,n]]}]

Stated another way, the exact power of a prime which divides is

(6)

where is the digit sum of in base (Boros and Moll 2004, p. 6). This can be implemented in the Wolfram Language as

  HighestPower2[p_Integer?PrimeQ, n_] :=
    (n - Total[IntegerDigits[n, p]])/(p - 1)

Therefore, as shown by Legendre,

(7)

(Havil 2003, p. 165).

Let be the last nonzero digit in , then the first few values are 2, 6, 4, 2, 2, 4, 2, 8, 8, 8, 6, 8, ... (OEIS A008904). This sequence was studied by Kakutani (1967), who showed that this sequence is "5-automatic," meaning roughly that there exists a finite automaton which, when given the digits of in base-5, will wind up in a state for which an output mapping specifies . The exact distribution of digits follows from this result.

Min Max Re Im

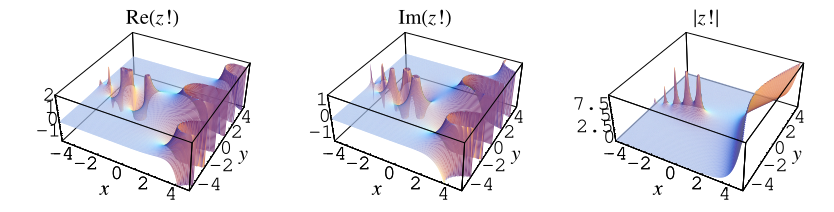
By noting that

(8)

where is the gamma function for integers , the definition can be generalized to complex values

(9)

This defines for all complex values of , except when is a negative integer, in which case is equal to complex infinity.

While Gauss (G1) introduced the notation

(10)

this notation was subsequently abandoned after Legendre introduced the gamma-notation (Edwards 2001, p. 8).

Using the identities for gamma functions, the values of (half integral values) can be written explicitly

			(11)
			(12)
			(13)
			(14)

where is a double factorial.

For integers and with ,

(15)

The logarithm of is frequently encountered

			(16)
			(17)
			(18)
			(19)
			(20)

where is the Euler-Mascheroni constant, is the Riemann zeta function, and is the polygamma function.

It is also given by the limit

			(21)
			(22)
			(23)
			(24)

where is the Pochhammer symbol.

where is the Euler-Mascheroni constant, is the Riemann zeta function, and is the polygamma function. The factorial can be expanded in a series

(25)

(OEIS A001163 and A001164). Stirling's series gives the series expansion for ,

			(26)
			(27)

(OEIS A046968 and A046969), where is a Bernoulli number.

In general, the power-product sequences (Mudge 1997) are given by . The first few terms of are 2, 5, 37, 577, 14401, 518401, ... (OEIS A020549), and is prime for , 2, 3, 4, 5, 9, 10, 11, 13, 24, 65, 76, ... (OEIS A046029). The first few terms of are 0, 3, 35, 575, 14399, 518399, ... (OEIS A046032), but is prime for only since for . The first few terms of are 0, 7, 215, 13823, 1727999, ... (OEIS A046033), and the first few terms of are 2, 9, 217, 13825, 1728001, ... (OEIS A019514).

The first few numbers such that the sum of the factorials of their digits is equal to the prime counting function are 6500, 6501, 6510, 6511, 6521, 12066, 50372, ... (OEIS A049529). This sequence is finite, with the largest term being .

Numbers such that

(28)

are called Wilson primes.

Brown numbers are pairs of integers satisfying the condition of Brocard's problem, i.e., such that

(29)

Only three such pairs are known: (5, 4), (11, 5), (71, 7). Erdős conjectured that these are the only three such pairs (Guy 1994, p. 193).