A digit sum
is a sum of the base-
digits of
.
The base-10 digit sum of the integer
is implemented in the Wolfram
Language as DigitSum[n], and the base-
digit sum as DigitSum[n, b].
The following table gives
for
, 2, ... and small
.
| OEIS | ||
| 2 | A000120 | 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, ... |
| 3 | A053735 | 1, 2, 1, 2, 3, 2, 3, 4, 1, 2, 3, 2, 3, 4, 3, ... |
| 4 | A053737 | 1, 2, 3, 1, 2, 3, 4, 2, 3, 4, 5, 3, 4, 5, 6, ... |
| 5 | A053824 | 1, 2, 3, 4, 1, 2, 3, 4, 5, 2, 3, 4, 5, 6, 3, ... |
| 6 | A053827 | 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 6, 2, 3, 4, 5, ... |
| 7 | A053828 | 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 7, 2, 3, ... |
| 8 | A053829 | 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 8, ... |
| 9 | A053830 | 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, ... |
| 10 | A007953 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, ... |
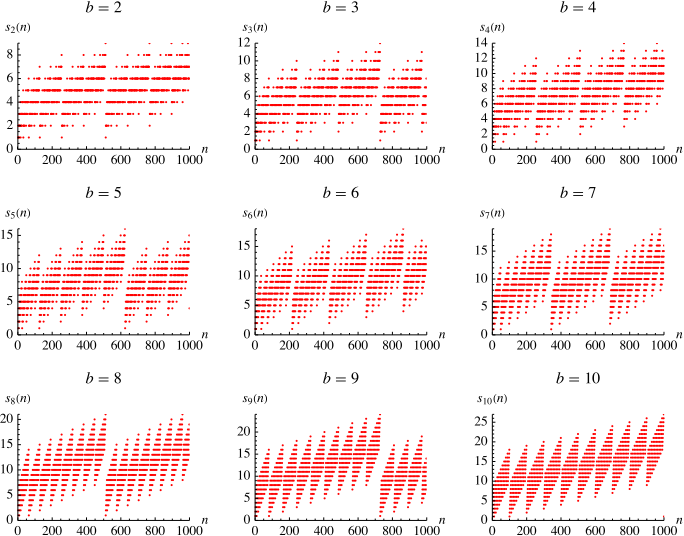
Plots of the digit sums of first thousand positive integers are illustrated above for bases 2 to 10.
Plotting
versus
and
gives the plot shown above.
The digits sum
satisfies the congruence
|
(1)
|
In base 10, this congruence is the basis of casting out nines and of fast divisibility tests such as those for 3 and 9.
satisfies the following unexpected
identity
|
(2)
|
the case of which was given in the 1981
Putnam competition (Allouche 1992). In addition,
|
(3)
| |||
![sum_(n=2)^(infty)[s_2(n)]^2(8n^3+4n^2+n-1)/(4n(n^2-1)(4n^2-1))](/images/equations/DigitSum/Inline21.svg) |
(4)
|
(OEIS A100044 and A100045; Allouche 1992, Allouche and Shallit 1992).
Let be the number of digit
blocks of 11 in the binary expansion of
, then
|
(5)
|
(OEIS A100046; Allouche 1992).
Sondow (2006) noted the unexpected identity
 |
(6)
|
The special case of
corresponds to a Thue-Morse sequence product
(J. Sondow, pers. comm., Oct. 31, 2006).
The numbers 1, 81, 1458 and 1729 (OEIS A110921) are each the product of their own digit sum and its reversal, for example , and
. These are the only four numbers with this property,
as proved by Fujiwara (Fujiwara and Ogawa 2005).