The first Brocard point is the interior point (also denoted
or
) of a triangle
with points labeled in counterclockwise order
for which the angles
,
, and
are equal, with the unique such angle denoted
. It is not a triangle
center, but has trilinear coordinates
|
(1)
|
(Kimberling 1998, p. 47).
Note that extreme care is needed when consulting the literature, since reversing the order in which the points of the triangle are labeled results in exchanging the Brocard points.
The second Brocard point is the interior point (also denoted
or
) for which the angles
,
, and
are equal, with the unique such angle denoted
. It is not a triangle
center, but has trilinear coordinates
|
(2)
|
(Kimberling 1998, p. 47).
Moreover, the two angles are equal, and this angle is called the Brocard
angle,
|
(3)
| |||
|
(4)
|
The first two Brocard points are isogonal conjugates (Johnson 1929, p. 266). They were described by French army officer Henri Brocard in 1875, although they had previously been investigated by Jacobi and, in 1816, Crelle (Wells 1991; Honsberger 1995, p. 98). They satisfy
 |
(5)
|
where
is the circumcenter,
is the circumradius, and
, where
is the circumcenter
and
is the Brocard angle (Honsberger 1995, p. 106).
The common statement (Bernhart 1959; Wells 1991, pp. 21-22; Marshall et al. 2005) attributed to Brocard in response to an 1877 question from Edouard Lucas,
namely that if three dogs start at the vertices of a triangle and chase either their
left or right neighbor at a constant speed, the three will meet at either or
, is incorrect. This can be seen by considering an isosceles triangle that is nearly collinear and
noting that two of the dogs will need to go much further than the other dog and so
can't be traveling at the same speed (cf. Peterson 2001, Nester) in order to meet
the other two at one of the points
or
.
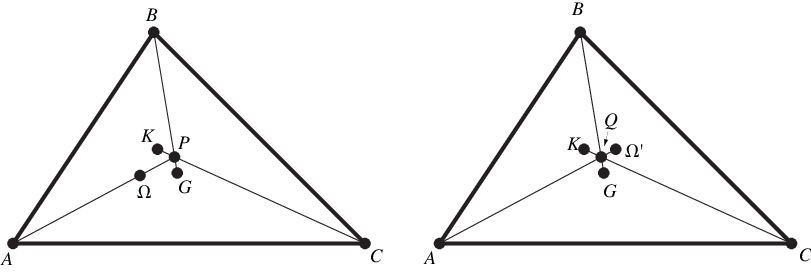
One Brocard line, triangle median, and symmedian (out of the three of each)
are concurrent, with ,
, and
meeting at a point, where
is the triangle centroid
and
is the symmedian point. Similarly,
,
, and
meet at a point which is the isogonal
conjugate of the first (Johnson 1929, pp. 268-269; Honsberger 1995, pp. 121-124).
Let
be the circle which passes through the vertices
and
and is tangent to the line
at
, and similarly for
and
. Then the circles
,
, and
intersect in the first
Brocard point
.
Similarly, let
be the circle which passes through the vertices
and
and is tangent to the line
at
, and similarly for
and
. Then the circles
,
, and
intersect in the second
Brocard points
(Johnson 1929, pp. 264-265; Honsberger 1995, pp. 99-100).
The pedal triangles of and
are congruent, and similar
to the triangle
(Johnson 1929, p. 269). Lengths involving the
Brocard points include
|
(6)
|
|
(7)
|
Extend the segments ,
, and
to the circumcircle
of
to form
,
and the segments
,
, and
to form
. Then
and
are congruent to
(Honsberger 1995, pp. 104-106).
The third Brocard point is related to a given triangle by the triangle center function
|
(8)
|
(Casey 1893, Kimberling 1994) and is Kimberling center .
The third Brocard point
(or
or
)
is collinear with the Spieker
center and the isotomic conjugate of its
triangle's incenter.