If 
moves along a known curve, then 
describes a pursuit curve if 
is always directed toward 
and 
and 
move with uniform velocities. Pursuit curves were considered
in general by the French scientist Pierre Bouguer in 1732, and subsequently by the
English mathematician Boole.
Under the name "path minimization," pursuit curves are alluded to by math genius Charlie Eppes in the Season 2 episode "Dark Matter" of the television crime drama NUMB3RS when considering the actions of the mysterious third shooter.
The equations of pursuit are given by
 |
(1)
|
which specifies that the tangent vector at point 
is always parallel to the line connecting
and 
, combined with
 |
(2)
|
which specifies that the point 
moves with constant speed (without loss of generality, taken
as unity above). Plugging (2) into (1) therefore
gives
 |
(3)
|
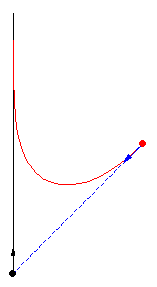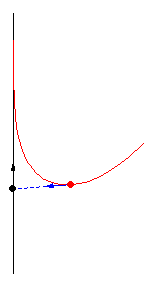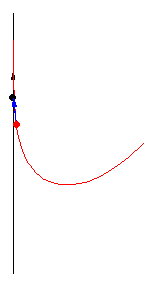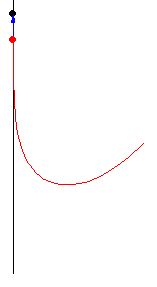
The case restricting 
to a straight line was studied by Arthur Bernhart (MacTutor Archive). Taking the
parametric equation of 
and the equation of the point 
to be 
, the equations of motion for this problem are given
by
![1/(sqrt(x^2+(t-y)^2))[0-x; t-y]·[x^.; y^.]=1](/images/equations/PursuitCurve/NumberedEquation4.svg) |
(4)
|
and
 |
(5)
|
Squaring and rearranging (4) gives
![[(t-y)y^.-xx^.]^2=x^2+(t-y)^2.](/images/equations/PursuitCurve/NumberedEquation6.svg) |
(6)
|
Expanding gives
 |
(7)
|
which can be simplified using (5) to
 |
(8)
|
But this is a perfect square,
![[xy^.+(t-y)x^.]^2=0,](/images/equations/PursuitCurve/NumberedEquation9.svg) |
(9)
|
so taking the square root of both sides gives
 |
(10)
|
This equation can be converted into one for 
as a function of 
by dividing both sides by 
, giving
 |
(11)
|
where 
.
To eliminate 
,
note that the arc length traveled by 
is given by
 |
(12)
|
since 
is a constant for this problem, so (11) becomes
 |
(13)
|
Differentiating then gives a second-order ordinary differential equation
 |
(14)
|
that can be solved analytically to yield
 |
(15)
|
As expected, the solution in involves two arbitrary constants 
and 
whose values are fixed by the initial conditions.
The initial conditions for a particle starting at 
at time 
are given by
 |  |  |
(16)
|
 |  |  |
(17)
|
Plugging these into (15), solving for 
and 
, and plugging the results back into (15)
gives the full solution
![y=1/4[(y_0+r_0)eta+(y_0-r_0)lneta+3y_0-r_0],](/images/equations/PursuitCurve/NumberedEquation16.svg) |
(18)
|
where
 |  |  |
(19)
|
 |  |  |
(20)
|
The point at which the 
-component
of 
's motion changes direction (corresponding
to the minimum of 
,
where 
turns and begin following the chase point from behind it) can be found by differentiating
(18) with respect to 
, setting equal to 0, and solving for 
. The result is
 |
(21)
|
Plugging in and simplifying gives the corresponding 
-coordinate,
 |
(22)
|
It is also possible to express the solution in closed form for 
and 
. Plugging (◇) into (◇) and solving for 
gives
![t=xy^'-y=1/4[(eta-1)(r_0+y_0)+(r_0-y_0)lneta],](/images/equations/PursuitCurve/NumberedEquation19.svg) |
(23)
|
which can be inverted in terms of the Lambert W-function to obtain
 |
(24)
|
where
 |
(25)
|
Plugging this in to the equation for 
then gives
![y(t)=1/4[3y_0-r_0+(y_0-r_0)ln((W(chie^(chi-4t/(r_0-y_0))))/chi)+(y_0+r_0)(W(chie^(chi-4t/(r_0-y_0))))/chi].](/images/equations/PursuitCurve/NumberedEquation22.svg) |
(26)
|
|
|
|
|
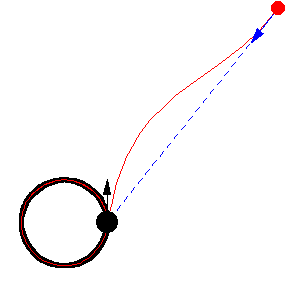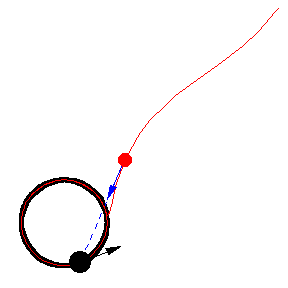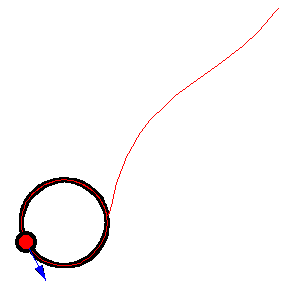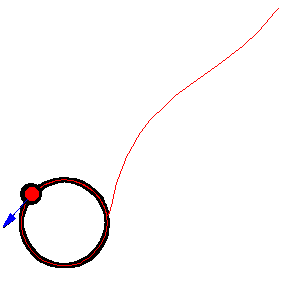
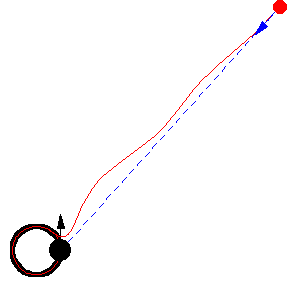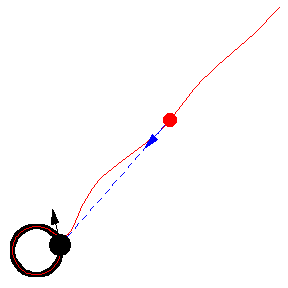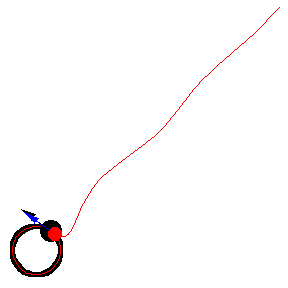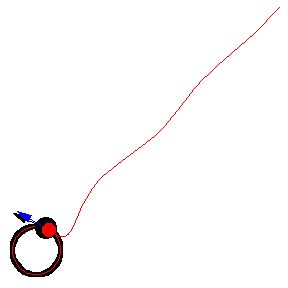
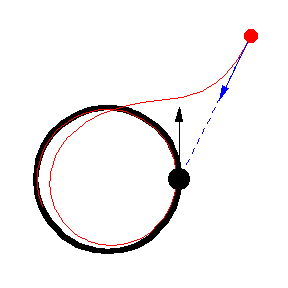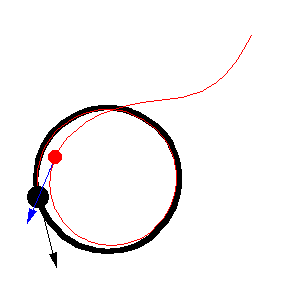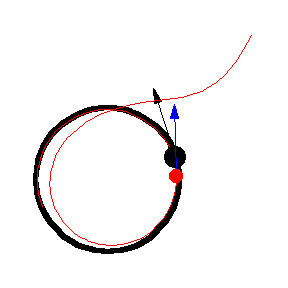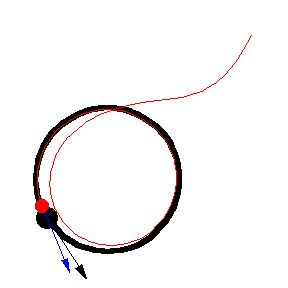
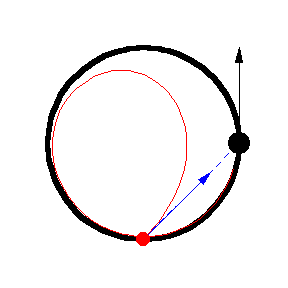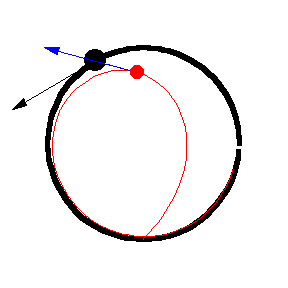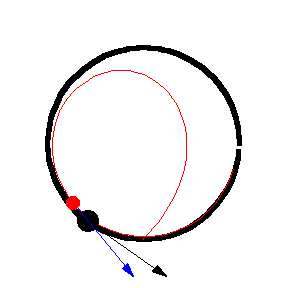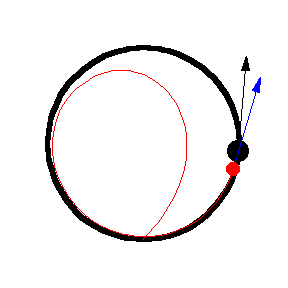
The figures above show various pursuit curves for 
moving about a circle at constant speed.
The problem of 
mice (or dogs) starting at the corners of a regular polygon and running towards each
other is called the mice problem.
