Branch Cut

A branch cut is a curve (with ends possibly open, closed, or half-open) in the complex plane across which an analytic multivalued function is discontinuous. For convenience, branch cuts are often taken as lines or line segments. Branch cuts (even those consisting of curves) are also known as cut lines (Arfken 1985, p. 397), slits (Kahan 1987), or branch lines.

For example, consider the function which maps each complex number to a well-defined number . Its inverse function , on the other hand, maps, for example, the value to . While a unique principal value can be chosen for such functions (in this case, the principal square root is the positive one), the choices cannot be made continuous over the whole complex plane. Instead, lines of discontinuity must occur. The most common approach for dealing with these discontinuities is the adoption of so-called branch cuts. In general, branch cuts are not unique, but are instead chosen by convention to give simple analytic properties (Kahan 1987). Some functions have a relatively simple branch cut structure, while branch cuts for other functions are extremely complicated.

An alternative to branch cuts for representing multivalued functions is the use of Riemann surfaces.

In addition to branch cuts, singularities known as branch points also exist. It should be noted, however, that the endpoints of branch cuts are not necessarily branch points.

Branch cuts do not arise for the single-valued trigonometric, hyperbolic, integer power, and exponential functions. However, their multivalued inverses do require branch cuts. The plots and table below summarize the branch cut structure of inverse trigonometric, inverse hyperbolic, noninteger power, and logarithmic functions adopted in the Wolfram Language.

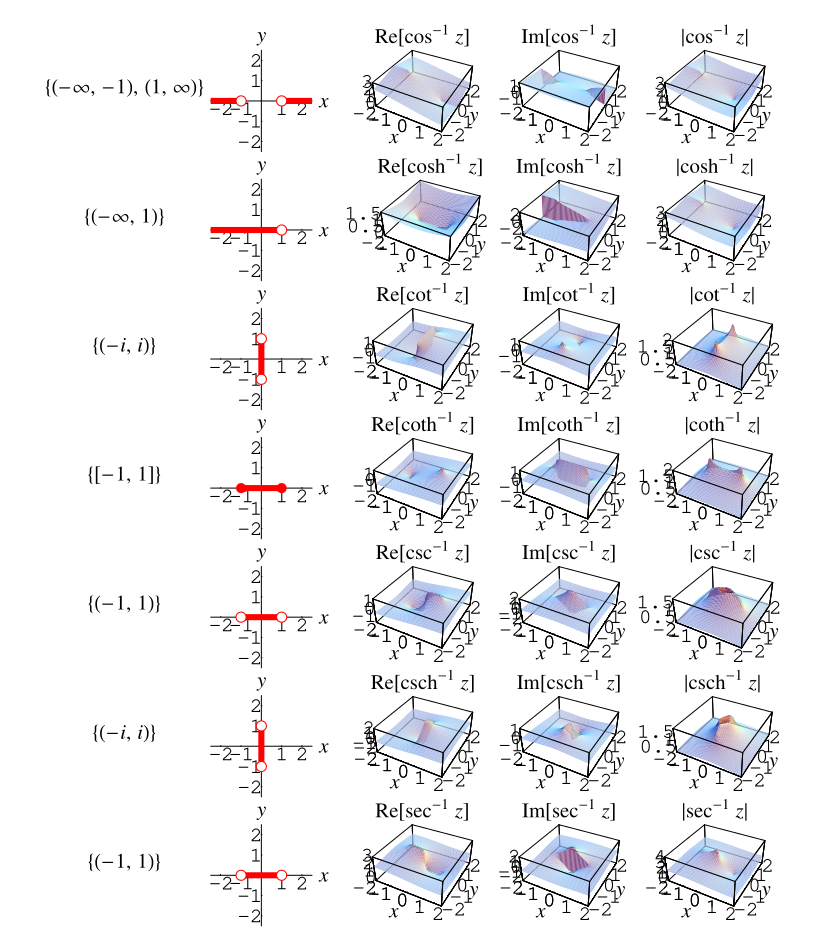
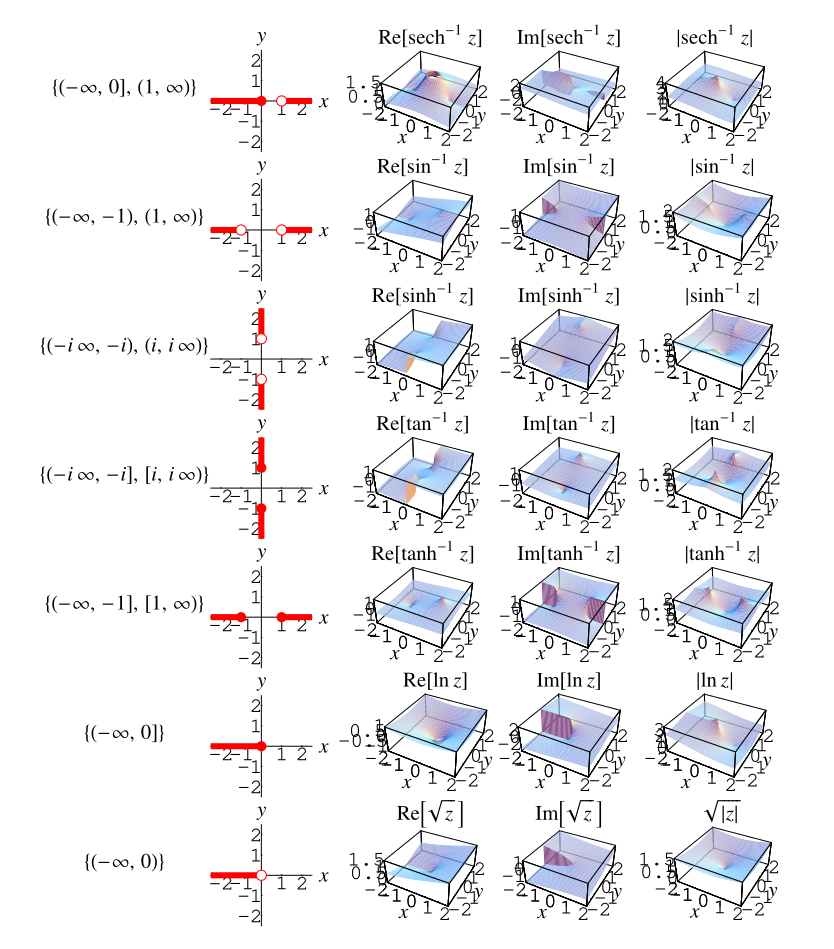
function name	function	branch cut(s)
inverse cosecant
inverse cosine		and
inverse cotangent
inverse hyperbolic cosecant
inverse hyperbolic cosine
inverse hyperbolic cotangent
inverse hyperbolic secant		and
inverse hyperbolic sine		and
inverse hyperbolic tangent		and
inverse secant
inverse sine		and
inverse tangent		and
natural logarithm
power		for ; for
square root