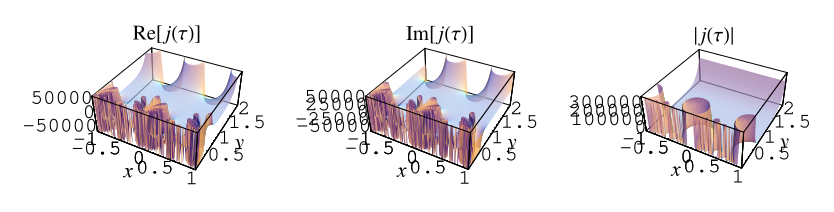
The -function is the modular function defined
by
|
(1)
|
where is the half-period
ratio,
,
![J(tau)=4/(27)([1-lambda(tau)+lambda^2(tau)]^3)/(lambda^2(tau)[1-lambda(tau)]^2)](/images/equations/j-Function/NumberedEquation2.svg) |
(2)
|
is Klein's absolute invariant, is the elliptic
lambda function
 |
(3)
|
|
(4)
|
is the nome, and .
Gauss was apparently aware of the -function before 1800. Hermite used it in solving the quintic
in about 1858. Dedekind gave a nice definition in about 1877, and Klein studied the
function beginning in 1879 or 1880. The
-function is related to the factors of the group
order of the monster group and to supersingular
primes (Ogg 1980).
This function can also be specified in terms of the Weber functions ,
,
,
,
and
as
![([f^(24)(tau)-16]^3)/(f^(24)(tau))](/images/equations/j-Function/Inline16.svg) |
(5)
| ||
![([f_1^(24)(tau)+16]^3)/(f_1^(24)(tau))](/images/equations/j-Function/Inline19.svg) |
(6)
| ||
![([f_2^(24)(tau)+16]^3)/(f_2^(24)(tau))](/images/equations/j-Function/Inline22.svg) |
(7)
| ||
|
(8)
| |||
|
(9)
|
(Weber 1979, p. 179; Atkin and Morain 1993).
The -function is an analytic
function on the upper half-plane which is
invariant with respect to the special linear group
. It has a Fourier
series
|
(10)
|
where
|
(11)
|
is therefore related
via
|
(12)
|
The coefficients in the expansion of the -function satisfy:
1. for
and
,
2. all s
are integers with fairly limited growth with respect
to
, and
3. is an algebraic
number, sometimes a rational number, and sometimes
even an integer at certain very special values of
.
The latter result is the end result of the massive and beautiful theory of complex multiplication and the first step of Kronecker's so-called "Jugendtraum."
Therefore all of the coefficients in the Laurent series
 |
(13)
|
(OEIS A000521) are positive integers (Rankin 1977, Apostol 1997). Berwick (1916) calculated the first seven
, Zuckerman (1939) found the first
24, and van Wijngaarden (193) gave the first 100.
Some remarkable sum formulas involving for
, where
is the upper half-plane,
and
include
![([1+240sum_(n=1)^(infty)sigma_3(n)q^_^n]^3)/(q^_product_(n=1)^(infty)(1-q^_^n)^(24))](/images/equations/j-Function/Inline48.svg) |
(14)
| ||
 |
(15)
| ||
![([theta_2^8(sqrt(q^_))+theta_3^8(sqrt(q^_))+theta_2^4(sqrt(q^_))]^3)/(8q^_(q^_)_infty^(24)),](/images/equations/j-Function/Inline54.svg) |
(16)
|
where
is an Eisenstein series,
is a q-Pochhammer
symbol, and
![[-1+504sum_(n=1)^inftysigma_5(n)q^_^n]^2=[j(q^_)-12^3]sum_(n=1)^inftytau(n)q^_^n,](/images/equations/j-Function/NumberedEquation9.svg) |
(17)
|
where
is the divisor function, and
is the tau function (not
to be confused with the half-period ratio
). In addition,
![504^2[-2/(504)sigma_5(n)+sum_(k=1)^(n-1)sigma_5(k)sigma_5(n-k)]
=tau(n+1)-984tau(n)+sum_(k=1)^(n-1)c(k)tau(n-k)
(65520)/(691)[sigma_(11)(n)-tau(n)]
=tau(n+1)+24tau(n)+sum_(k=1)^(n-1)c(k)tau(n-k)](/images/equations/j-Function/NumberedEquation10.svg) |
(18)
|
(Lehmer 1942; Apostol 1997, p. 92). These are closely related to Eisenstein series.
Equation (18) leads immediately to the remarkable congruence
|
(19)
|
Lehmer (1942) showed that
|
(20)
|
for all ,
and Lehner (1949ab) and Apostol (1997, pp. 22, 74, and 90-91) demonstrated that
|
(21)
| |
|
(22)
| |
|
(23)
| |
|
(24)
| |
|
(25)
|
More generally,
|
(26)
| |
|
(27)
| |
|
(28)
| |
|
(29)
|
(Lehner 1949ab; Apostol 1997, p. 91). Congruences of this type cannot exist for 13, but Newman (1958) showed
|
(30)
|
where
and
if
is not an integer (Apostol 1997, p. 91). Congruences
for
have been generalized by Atkin and
O'Brien (1967).
An asymptotic formula for
was discovered by Petersson (1932), and subsequently independently rediscovered by
Rademacher (1938):
 |
(31)
|
Let be a squarefree positive integer, and define the half-period
ratio by
 |
(32)
|
so
 |
(33)
|
It then turns out that
is an algebraic integer of degree
, where
is the class number of
the binary quadratic form discriminant
of the quadratic
field
(Silverman 1986; Berndt 1994, p. 90).
If , then
is an algebraic integer
of degree 1, i.e., just a plain integer. Furthermore,
the integer is a perfect cube.
But these are precisely the Heegner numbers
,
,
,
,
,
,
,
,
.
The exact values of
corresponding to the Heegner numbers are
|
(34)
| |||
|
(35)
| |||
|
(36)
| |||
|
(37)
| |||
|
(38)
| |||
|
(39)
| |||
|
(40)
| |||
|
(41)
| |||
|
(42)
|
The positions of these special values of are illustrated above. (Note the curious though not particularly
significant fact that number 5280 is also the number of feet in a mile.)
The greater (in absolute value) the Heegner number ,
the closer to an integer is the expression
, since the initial term in
is the largest and subsequent terms are the smallest.
The best approximations with
are therefore
|
(43)
| |||
|
(44)
| |||
|
(45)
|
(the latter of which appears in Trott 2004, p. 8). The almost integer generated by the last of these, (corresponding to the field
and the imaginary
quadratic field of maximal discriminant), is sometimes known as the Ramanujan
constant. However, this attribution is historically fallacious since this amazing
property of
was first noted by Hermite (1859) and does not seem to appear in any of the works
of Ramanujan.
There are 18 numbers having class number , with the odd discriminants not divisible by three corresponding
to the exact values
|
(46)
| |||
|
(47)
| |||
|
(48)
| |||
|
(49)
| |||
|
(50)
| |||
|
(51)
| |||
|
(52)
|
and even
for
, 10, 13, 22, 37, 58,
|
(53)
| |||
|
(54)
| |||
|
(55)
| |||
|
(56)
| |||
|
(57)
| |||
|
(58)
|
and discriminants divisible by 3,
|
(59)
| |||
|
(60)
| |||
|
(61)
| |||
|
(62)
| |||
|
(63)
|
with the square factor being a fundamental unit.
The best approximations for are, for even discriminants,
|
(64)
|
and for odd discriminants,
 |
(65)
|
The numbers
|
(66)
| |||
|
(67)
| |||
|
(68)
|
are also almost integers. These correspond to binary quadratic forms with discriminants ,
,
and
, which are the largest (in absolute
value) discriminants with class number two that are
divisible by 4. They were noted by Ramanujan (Berndt 1994, pp. 88-91).