TOPICS
Search

Klein's Absolute Invariant

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
KleinJReal
Min Max
Powered by webMathematica
KleinJReImAbs
Min Max
Re
Im Powered by webMathematica

Let omega_1 and omega_2 be periods of a doubly periodic function, with tau=omega_2/omega_1 the half-period ratio a number with I[tau]!=0. Then Klein's absolute invariant (also called Klein's modular function) is defined as

J(omega_1,omega_2)=(g_2^3(omega_1,omega_2))/(Delta(omega_1,omega_2)),
(1)

where g_2 and g_3 are the invariants of the Weierstrass elliptic function with modular discriminant

Delta=g_2^3-27g_3^2
(2)

(Klein 1877). If tau in H, where H is the upper half-plane, then

J(tau)=J(1,tau)=J(omega_1,omega_2)
(3)

is a function of the ratio tau only, as are g_2, g_3, and Delta. Furthermore, g_2(tau), g_3(tau), Delta(tau), and J(tau) are analytic in H (Apostol 1997, p. 15).

Klein's absolute invariant is implemented in the Wolfram Language as KleinInvariantJ[tau].

The function J(tau) is the same as the j-function, modulo a constant multiplicative factor.

Every rational function of J is a modular function, and every modular function can be expressed as a rational function of J (Apostol 1997, p. 40).

Klein's invariant can be given explicitly by

J(tau)=4/(27)([1-lambda(tau)+lambda^2(tau)]^3)/(lambda^2(tau)[1-lambda(tau)]^2)
(4)
=([E_4(tau)]^3)/([E_4(tau)]^3-[E_6(tau)^2])
(5)

(Klein 1878-1879, Cohn 1994), where lambda(tau) is the elliptic lambda function

lambda(tau)=[(theta_2(0,q))/(theta_3(0,q))]^4,
(6)

theta_i(0,q) is a Jacobi theta function, the E_i(tau) are Eisenstein series, and q is the nome. Klein's invariant can also be simply expressed in terms of the five Weber functions f(tau), f_1(tau), f_2(tau), gamma_2(tau), and gamma_3(tau).

J(tau) is invariant under a unimodular transformation, so

J((atau+b)/(ctau+d))=J(tau),
(7)

and J(tau) is a modular function. J(tau) takes on the special values

J(rho=e^(2pii/3))=0
(8)
J(i)=1
(9)
J(iinfty)=infty.
(10)

J(tau) satisfies the functional equations

J(tau)=J(tau+1)
(11)
J(tau)=J(-1/tau).
(12)

It satisfies a number of beautiful multiple-argument identities, including the duplication formula

J(tau)=f(t)
(13)
J(2tau)=f(1/t)
(14)

with

t=1/(64)[(eta(tau))/(eta(2tau))]^(24)
(15)
f(u)=((u+4)^3)/(27u^2)
(16)

and eta(z) the Dedekind eta function, the triplication formula

J(tau)=g(t)
(17)
J(3tau)=g(1/t),
(18)

with

t=1/(27)[(eta(tau))/(eta(3tau))]^(12)
(19)
g(u)=((u+1)(u+9)^3)/(64u^3),
(20)

and the quintuplication formula

1728J(tau)=h(t)
(21)
1728J(5tau)=h(5/t),
(22)

with

t=1/5[(eta(tau))/(eta(5tau))]^6
(23)
h(u)=(5(u^2+50u+125)^3)/(u^5).
(24)
KleinsAbsoluteInvariantPic

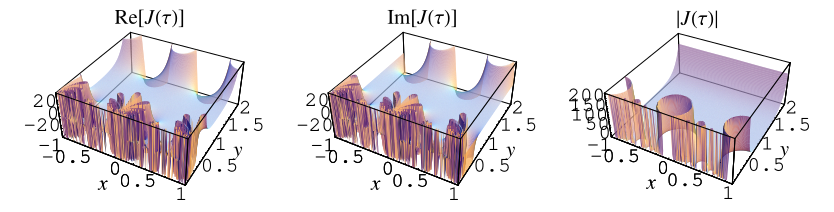
Plotting the real or imaginary part of J(tau) in the complex plane produces a beautiful fractal-like structure, illustrated above.

See also

Elliptic Lambda Function, Eisenstein Series, j-Function, Jacobi Theta Functions, Pi, Weber Functions

Related Wolfram sites

http://functions.wolfram.com/EllipticFunctions/KleinInvariantJ/

Explore with Wolfram|Alpha

References

Apostol, T. M. "Klein's Modular Function J(tau)," "Invariance of J Under Unimodular Transformation," "The Fourier Expansions of Delta(tau) and J(tau)," "Special Values of J," and "Modular Functions as Rational Functions of J." §1.12-1.13, 1.15, and 2.5-2.6 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 15-18, 20-22, and 39-40, 1997.Brezhnev, Y. V. "Uniformisation: On the Burnside Curve y^2=x^5-x." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 115 and 179, 1987.Cohn, H. Introduction to the Construction of Class Fields. New York: Dover, p. 73, 1994.Klein, F. "Sull' equazioni dell' Icosaedro nella risoluzione delle equazioni del quinto grado [per funzioni ellittiche]." Reale Istituto Lombardo, Rendiconto, Ser. 2 10, 1877.Klein, F. "Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades." Math. Ann. 14, 111-172, 1878-1879.Nesterenko, Yu. V. A Course on Algebraic Independence: Lectures at IHP 1999. Unpublished manuscript. 1999.

Referenced on Wolfram|Alpha

Klein's Absolute Invariant

Cite this as:

Weisstein, Eric W. "Klein's Absolute Invariant." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/KleinsAbsoluteInvariant.html

Subject classifications