A parabola (plural "parabolas"; Gray 1997, p. 45) is the set of all points in the plane equidistant from a given line (the conic
section directrix) and a given point
not on the line (the focus). The
focal parameter (i.e., the distance between the
directrix and focus) is therefore given by
, where
is the distance from the vertex to the directrix or focus.
The surface of revolution obtained by rotating
a parabola about its axis of symmetry is called a paraboloid.
The parabola was studied by Menaechmus in an attempt to achieve cube duplication. Menaechmus solved the problem by finding the intersection of the
two parabolas
and
. Euclid wrote about the parabola,
and it was given its present name by Apollonius. Pascal considered the parabola as
a projection of a circle, and Galileo showed that projectiles
falling under uniform gravity follow parabolic paths. Gregory and Newton considered
the catacaustic properties of a parabola that bring
parallel rays of light to a focus (MacTutor Archive), as illustrated above.
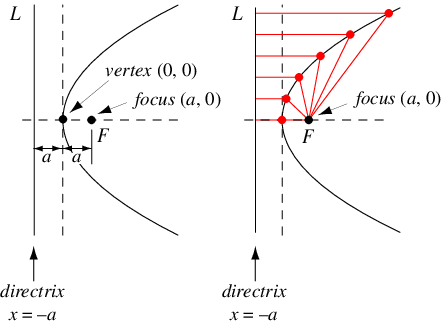
For a parabola opening to the right with vertex at (0, 0), the equation in Cartesian coordinates is
|
(1)
|
|
(2)
|
|
(3)
|
|
(4)
|
The quantity
is known as the latus rectum.
If the vertex is at
instead of (0, 0), the equation of the parabola with latus
rectum
is
|
(5)
|
A parabola opening upward with vertex is at and latus rectum
has equation
|
(6)
|
Three points uniquely determine one parabola with directrix parallel to the -axis and one with directrix parallel
to the
-axis. If these parabolas pass through
the three points
,
, and
, they are given by equations
 |
(7)
|
and
 |
(8)
|
In polar coordinates, the equation of a parabola with parameter
and center (0, 0) is given by
|
(9)
|
(left figure). The equivalence with the Cartesian form can be seen by setting up a coordinate system
and plugging in
and
to obtain
 |
(10)
|
Expanding and collecting terms,
|
(11)
|
so solving for
gives (◇). A set of confocal parabolas is shown in the figure on the right.
In pedal coordinates with the pedal point at the focus, the equation is
|
(12)
|
The parabola can be written parametrically as
|
(13)
| |||
|
(14)
|
or
|
(15)
| |||
|
(16)
|
A segment of a parabola is a Lissajous curve.
A parabola may be generated as the envelope of two concurrent line segments by connecting opposite points on the two lines (Wells 1991).
In the above figure, the lines ,
,
and
are tangent to the parabola at points
,
, and
,
respectively. Then
(Wells 1991). Moreover, the circumcircle of
passes through the focus
(Honsberger 1995, p. 47). In addition,
the foot of the perpendicular to a tangent to a parabola from the focus
always lies on the tangent at the vertex (Honsberger 1995, p. 48).
Given an arbitrary point
located "outside" a parabola, the tangent or tangents to the parabola through
can be constructed by drawing the circle having
as a diameter, where
is the focus. Then locate the points
and
at which the circle cuts the vertical
tangent through
.
The points
and
(which can collapse to a single point
in the degenerate case) are then the points of tangency of the lines
and
and the parabola (Wells 1991).
The curvature, arc length, and tangential angle are
 |
(17)
| ||
|
(18)
| |||
|
(19)
|
The tangent vector of the parabola is
|
(20)
| |||
|
(21)
|
The plots below show the normal and tangent vectors to a parabola.