Given a parabola with parametric
equations
the negative pedal curve for a pedal point
Taking the pedal point at the origin
which is a semicubical parabola . Similarly, taking
which is a Tschirnhausen cubic .
See also Negative Pedal Curve ,
Parabola ,
Parabola Pedal
Curve ,
Tschirnhausen Cubic
Explore with Wolfram|Alpha
References Ameseder, A. "Negative Fusspunktcurven der Kegelschnitte." Archiv Math. u. Phys. 64 , 170-176, 1879. Lockwood, E. H.
A
Book of Curves. Referenced on Wolfram|Alpha Parabola Negative Pedal Curve
Cite this as:
Weisstein, Eric W. "Parabola Negative Pedal
Curve." From MathWorld https://mathworld.wolfram.com/ParabolaNegativePedalCurve.html
Subject classifications
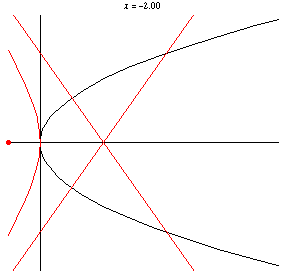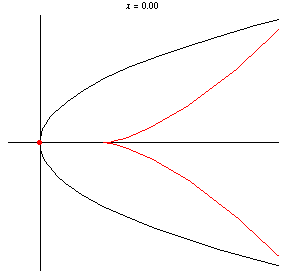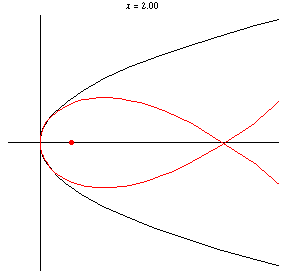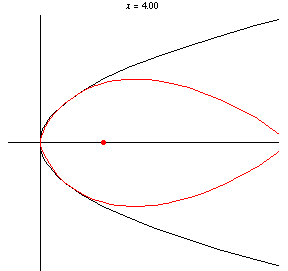
has equation
gives
gives