The function
giving the fractional (noninteger) part of a real number
. The symbol
is sometimes used instead of
(Graham et al. 1994, p. 70; Havil 2003,
p. 109), but this notation is not used in this work due to possible confusion
with the set containing the element
.
Unfortunately, there is no universal agreement on the meaning of for
and there are two common definitions. Let
be the floor function,
then the Wolfram Language command
FractionalPart[x]
is defined as
![frac(x)={x-|_x_| x>=0; x-[x] x<0](/images/equations/FractionalPart/NumberedEquation1.svg) |
(1)
|
(left figure). This definition has the benefit that , where
is the integer part of
. Although Spanier and Oldham (1987) use
the same definition as the Wolfram Language,
they mention the formula only very briefly and then say it will not be used further.
Graham et al. (1994, p. 70), and perhaps most other mathematicians, use
the different definition
|
(2)
|
(right figure).
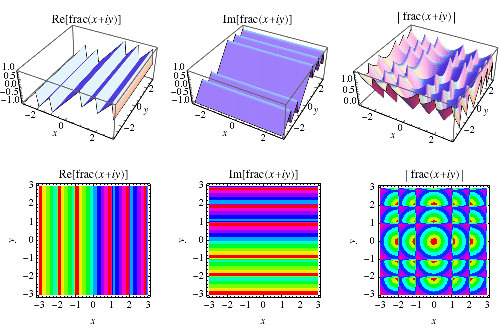 |
The fractional part function can also be extended to the complex plane as
|
(3)
|
as illustrated above.
Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used. Here, S&O indicates Spanier and Oldham (1987).
| notation | name | S&O | Graham et al. | Wolfram Language |
| ceiling function | -- | ceiling, least integer | Ceiling[x] | |
| congruence | -- | -- | Mod[m, n] | |
| floor function | floor, greatest integer, integer part | Floor[x] | ||
| fractional value | fractional
part or | SawtoothWave[x] | ||
| fractional part | no name | FractionalPart[x] | ||
| integer part | no name | IntegerPart[x] | ||
| nearest integer function | -- | -- | Round[x] | |
| quotient | -- | -- | Quotient[m, n] |
The (possibly scaled) periodic waveform corresponding to the latter definition is known as the sawtooth wave.
The fractional part of ,
illustrated above, has the interesting analytic integrals
|
(4)
| |||
|
(5)
| |||
|
(6)
| |||
|
(7)
| |||
|
(8)
| |||
|
(9)
|
The integral
|
(10)
|
is therefore a telescoping sum given by
![lim_(n->infty)[lnn-sum_(k=2)^(n)1/k]](/images/equations/FractionalPart/Inline46.svg) |
(11)
| ||
|
(12)
| |||
|
(13)
|
where
is the Euler-Mascheroni constant and
is the harmonic
number.
An additional related integral that can be done in closed form and gives the same result is
|
(14)
|
(Havil 2003, pp. 109-111).
The plot above shows the fractional parts of for
, showing characteristic gaps (Trott 2004, p. 223).
A consequence of Weyl's criterion is that the sequence
is dense and equidistributed in the interval
for irrational
, where
, 2, ... (Finch 2003).