Excentral Triangle

The excentral triangle, also called the tritangent triangle, of a triangle is the triangle with vertices corresponding to the excenters of .

It is the anticevian triangle with respect to the incenter (Kimberling 1998, p. 157), and also the antipedal triangle with respect to .

The circumcircle of the excentral triangle is the Bevan circle.

Its trilinear vertex matrix is

(1)

The excentral triangle has side lengths

			(2)
			(3)
			(4)

and area

			(5)
			(6)

where , , and are the area, inradius, and semiperimeter of the original triangle , respectively. It therefore has the same side lengths and area as the hexyl triangle.

The excentral triangle is perspective to every Cevian triangle (Kimberling 1998, p. 157).

The excentral-hexyl ellipse passes through the vertex of the excentral and hexyl triangles.

Beginning with an arbitrary triangle , find the excentral triangle . Then find the excentral triangle of that triangle, and so on. Then the resulting triangle approaches an equilateral triangle (Johnson 1929, p. 185; Goldoni 2003). The analogous result also holds for iterative construction of contact triangles (Goldoni 2003).

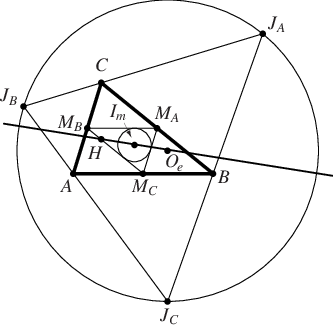
Given a triangle , draw the excentral triangle and medial triangle . Then the orthocenter of , incenter of , and circumcenter of are collinear with the midpoint of (Honsberger 1995).

The incenter of coincides with the orthocenter of , and the circumcenter of coincides with the nine-point center of . Furthermore, is the midpoint of the line segment joining the orthocenter and circumcenter of (Honsberger 1995).

The following table gives the centers of the excentral triangle in terms of the centers of the reference triangle for Kimberling centers with .

	center of excentral triangle		center of reference triangle
	incenter		incenter of excentral triangle
	triangle centroid		triangle centroid of the excentral triangle
	circumcenter		Bevan point
	orthocenter		incenter
	nine-point center		circumcenter
	symmedian point		mittenpunkt
	Gergonne point		Gergonne point of excentral triangle
	Nagel point		Nagel point of excentral triangle
	mittenpunkt		mittenpunkt of excentral triangle
	first isodynamic point		third Evans perspector
	second isodynamic point		second Evans perspector
	Clawson point		congruent isoscelizers point
	perspector of abc and orthic-of-orthic triangle		-Ceva conjugate of
	homothetic center of orthic and tangential triangles		isogonal conjugate of
	Euler infinity point		isogonal conjugate of
	second power point		congruent circumcircles isoscelizer point
	third power point		-Ceva conjugate of
	perspector of the orthic and intangents triangles		congruent incircles isoscelizer point
	-Ceva conjugate of		third isoscelizer point
	crosspoint of and		second isoscelizer point
	triangle centroid of orthic triangle		triangle centroid
	orthocenter of orthic triangle		orthocenter
	symmedian point of orthic triangle		symmedian point
	Kosnita point		-Ceva conjugate of
	isogonal conjugate of		equal perimeters isoscelizer point
	isogonal conjugate of		intersection of lines and
	isogonal conjugate of		eigentransform of
	orthocenter of the contact triangle		second mid-arc point of anticomplementary triangle
	Prasolov point		intersection of lines and
	symmedian point of the anticomplementary triangle		excentral isogonal conjugate of
	isotomic conjugate of incenter		intersection of lines and
	third Brocard point		-aleph conjugate of
	Cevapoint of incenter and Clawson point		first isoscelizer point
	Cevapoint of triangle centroid and circumcenter		excentral isogonal conjugate of
	isogonal conjugate of		excentral isogonal conjugate of
	isogonal conjugate of		excentral isogonal conjugate of
	Tarry point		5th Sharygin point