Given a triangle, extend two sides in the direction opposite their common vertex. The circle tangent to these
two lines and to the other side of the triangle is called
an excircle, or sometimes an escribed circle. The center of the excircle is called the excenter
and lies on the external angle bisector of the
opposite angle. Every triangle
has three excircles, and the trilinear coordinates
of the excenters are
,
,
and
. The radius
of the excircle
is called its exradius.
Note that the three excircles are not necessarily tangent to the incircle, and so these four circles are not equivalent to the configuration of the Soddy circles.
No Kimberling centers lie on any of the excircles.
Given a triangle with inradius , let
be the altitudes of the excircles,
and
their radii
(the exradii). Then
(Johnson 1929, p. 189).
There are four circles that are tangent all three sides (or their extensions) of a given triangle: the incircle and three excircles
,
,
and
. These four circles are, in turn,
all touched by the nine-point circle
. The incircle touches the nine-point circle at the Feuerbach
point
,
and the points of tangency with the excircles form the Feuerbach
triangle.
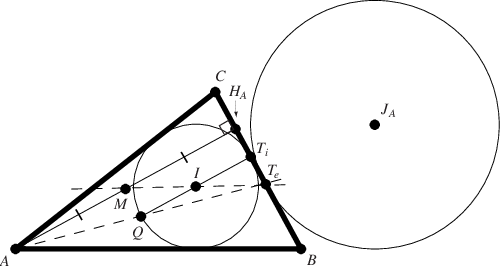
Given a triangle , construct the incircle
with incenter
and excircle with excenter
. Let
be the tangent point of
with its incircle,
be the tangent point of
with its excircle
,
the foot of the altitude to vertex
,
the midpoint of
, and construct
such that
is a diameter of the incircle.
Then
,
, and
are collinear, as are
,
,
and
(Honsberger 1995).