The Catalan numbers on nonnegative integers are a set of numbers that arise in tree
enumeration problems of the type, "In how many ways can a regular
-gon be divided into
triangles if different orientations
are counted separately?" (Euler's
polygon division problem). The solution is the Catalan number
(Pólya 1956; Dörrie 1965; Honsberger 1973;
Borwein and Bailey 2003, pp. 21-22), as graphically illustrated above (Dickau).
Catalan numbers are commonly denoted (Graham et al. 1994; Stanley 1999b, p. 219;
Pemmaraju and Skiena 2003, p. 169; this work) or
(Goulden and Jackson 1983, p. 111), and less commonly
(van Lint and Wilson 1992, p. 136).
Catalan numbers are implemented in the Wolfram Language as CatalanNumber[n].
The first few Catalan numbers for , 2, ... are 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796,
... (OEIS A000108).
Explicit formulas for
include
|
(1)
| |||
|
(2)
| |||
|
(3)
| |||
 |
(4)
| ||
|
(5)
| |||
|
(6)
| |||
|
(7)
|
where
is a binomial coefficient,
is a factorial,
is a double factorial,
is the gamma
function, and
is a hypergeometric function.
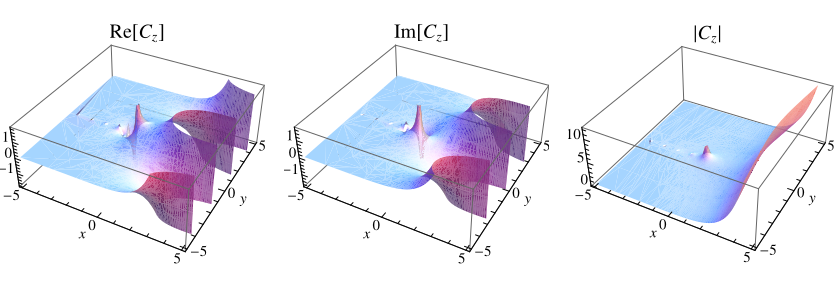
The Catalan numbers may be generalized to the complex plane, as illustrated above.
Sums giving
include
 |
(8)
| ||
 |
(9)
| ||
 |
(10)
| ||
 |
(11)
| ||
![sum_(k=0)^(|_n/2_|)[(n-2k+1)/(n-k+1)(n; n-k)]^2,](/images/equations/CatalanNumber/Inline51.svg) |
(12)
|
where
is the floor function, and a product for
is given by
 |
(13)
|
Sums involving
include the generating function
|
(14)
| |||
|
(15)
|
(OEIS A000108), exponential generating function
|
(16)
| |||
|
(17)
|
(OEIS A144186 and A144187), where
is a modified Bessel function
of the first kind, as well as
|
(18)
| |||
 |
(19)
|
The asymptotic form for the Catalan numbers is
|
(20)
|
(Vardi 1991, Graham et al. 1994).
The numbers of decimal digits in for
, 1, ... are 1, 5, 57, 598, 6015, 60199, 602051, 6020590,
... (OEIS A114466). The digits converge to
the digits in the decimal expansion of
(OEIS A114493).
A recurrence relation for is obtained from
|
(21)
|
so
|
(22)
|
Segner's recurrence formula, given by Segner in 1758, gives the solution to Euler's polygon division problem
|
(23)
|
With ,
the above recurrence relation gives the Catalan
number
.
From the definition of the Catalan number, every prime divisor of is less than
. On the other hand,
for
. Therefore,
is the largest Catalan prime, making
and
the only Catalan primes. (Of course, much more than this
can be said about the factorization of
.)
The only odd Catalan numbers are those of the form .
The first few are therefore 1, 5, 429, 9694845, 14544636039226909, ... (OEIS A038003).
The odd Catalan numbers
end in 5 unless the base-5 expansion of
uses only the digits 0, 1, 2, so it would be extremely
rare for a long sequence of essentially random base-5 digits to contain only in 0,
1, and 2. In fact, the last digits of the odd Catalan numbers are 1, 5, 9, 5, 9,
5, 9, 7, 5, 5, 5, 5, 5, ... (OEIS A094389),
so 5 is the last digit for all
up to at least
with the exception of 1, 3, 5, 7, and 8.
The Catalan numbers turn up in many other related types of problems. The Catalan number
also gives the number of binary bracketings
of
letters (Catalan's problem), the solution to
the ballot problem, the number of trivalent planted planar trees (Dickau; illustrated above),
the number of states possible in an
-flexagon, the number of different
diagonals possible in a frieze pattern with
rows, the number of Dyck
paths with
strokes, the number of ways of forming an
-fold exponential, the number of rooted planar binary trees
with
internal nodes, the number of rooted plane bushes with
graph edges, the number of extended
binary trees with
internal nodes, and the number of mountains which can be drawn
with
upstrokes and
downstrokes, the number of noncrossing handshakes possible across a round table between
pairs of people (Conway and Guy 1996)!
A generalization of the Catalan numbers is defined by
|
(24)
| |||
|
(25)
|
for
(Klarner 1970, Hilton and Pedersen 1991). The usual Catalan numbers
are a special case with
.
gives the number of
-ary trees with
source-nodes, the number of ways of associating
applications of a given
-ary operator, the number of ways
of dividing a convex polygon into
disjoint
-gons with nonintersecting polygon
diagonals, and the number of p-good paths
from (0,
)
to
(Hilton and Pedersen 1991).
A further generalization is obtained as follows. Let be an integer
, let
with
, and
. Then define
and let
be the number of p-good
paths from (1,
)
to
(Hilton and Pedersen 1991). Formulas for
include the generalized Jonah
formula
 |
(26)
|
and the explicit formula
|
(27)
|
A recurrence relation is given by
|
(28)
|
where ,
,
, and
(Hilton and Pedersen 1991).