The binomial coefficient is the number of ways of picking
unordered outcomes from
possibilities, also known as a combination
or combinatorial number. The symbols
and
are used to denote a binomial coefficient, and are sometimes
read as "
choose
."
therefore gives the number of k-subsets possible
out of a set of
distinct items. For example, The 2-subsets of
are the six pairs
,
,
,
,
, and
, so
. In addition, the number of lattice
paths from the origin
to a point
) is the binomial coefficient
(Hilton and Pedersen 1991).
The value of the binomial coefficient for nonnegative integers
and
with
is given by
|
(1)
|
(Graham et al. 1989, p.157), where denotes a factorial. Filling
in values by row for
, 1, ...,
for increasing
gives Pascal's triangle.
Writing the factorial as a gamma function
allows the binomial coefficient to be generalized to noninteger arguments (including
complex
and
)
as
|
(2)
|
The Roman coefficient (Roman 1992, Loeb 1995) is a generalization of the binomial coefficient. Whenever the binomial coefficient is defined, the Roman coefficient agrees with it. However, the Roman coefficients are defined for values for which the binomial coefficients are not.
Binomial coefficients for nonnegative integer give a polynomial in
|
(3)
| |||
|
(4)
|
where
is a Pochhammer symbol. These rational coefficients
are sometimes known as "generalized binomial coefficients."
Using the gamma function symmetry formula
|
(5)
|
for integer ,
and complex
,
this definition can be extended to negative integer arguments, making it continuous
at all integer arguments as well as continuous for all complex arguments except for
negative integer
and noninteger
,
in which case it is infinite (Kronenburg 2011). This definition, given by
 |
(6)
|
for negative integer and integer
is in agreement with the binomial theorem, and with combinatorial
identities with a few special exceptions (Kronenburg 2011).
The binomial coefficient is implemented in the Wolfram Language as Binomial[n,
k], which follows the above convention starting in Version 8. A variation
that preserves Pascal's identity
|
(7)
|
and which therefore differs in value for negative integer ,
is implemented in the Wolfram Language
as PascalBinomial[n, k].
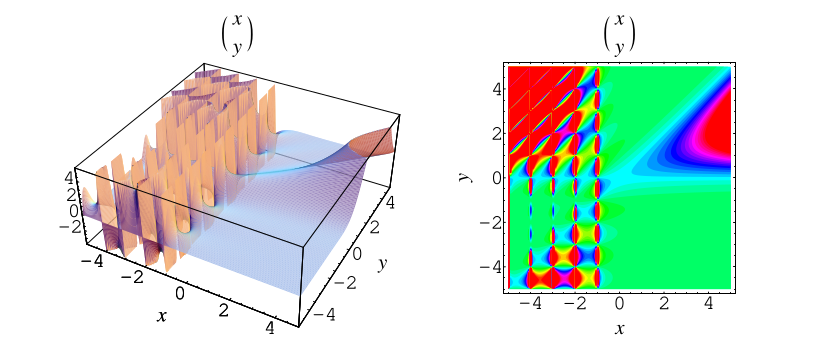
Plotting the binomial coefficient in the -plane (Fowler 1996) gives the beautiful plot shown above,
which has a very complicated graph for negative
and
and is therefore difficult to render using standard plotting
programs.
For a positive integer , the binomial theorem
gives
 |
(8)
|
The finite difference analog of this identity is known as the Chu-Vandermonde identity. A similar formula holds for negative integers,
 |
(9)
|
There are a number of elegant binomial sums.
The binomial coefficients satisfy the identities
|
(10)
| |||
|
(11)
| |||
|
(12)
| |||
|
(13)
|
The product of binomial coefficients is given by
 |
(14)
|
where
is a hyperfactorial and
is a factorial.
As shown by Kummer in 1852, if is the largest power of a prime
that divides
, where
and
are nonnegative integers, then
is the number of carries that occur
when
is added to
in base
(Graham et al. 1989, Exercise 5.36, p. 245; Ribenboim 1989; Vardi 1991,
p. 68). Kummer's result can also be stated in the form that the exponent of
a prime
dividing
is given by the number of integers
for which
|
(15)
|
where
denotes the fractional part of
. This inequality may be reduced to the study of the exponential
sums
,
where
is the Mangoldt function. Estimates of these
sums are given by Jutila (1973, 1974), but recent improvements have been made by
Granville and Ramare (1996).
R. W. Gosper showed that
|
(16)
|
for all primes, and conjectured that it holds only for primes. This was disproved when Skiena (1990)
found it also holds for the composite number . Vardi (1991, p. 63)
subsequently showed that
is a solution whenever
is a Wieferich prime and
that if
with
is a solution, then so is
. This allowed him to show that the only solutions
for composite
are 5907,
, and
, where 1093 and 3511 are Wieferich
primes.
Consider the binomial coefficients , the first few of which are 1, 3, 10, 35, 126,
... (OEIS A001700). The generating
function is
|
(17)
|
These numbers are squarefree only for , 3, 4, 6, 9, 10, 12, 36, ... (OEIS A046097),
with no others known. It turns out that
is divisible by 4 unless
belongs to a 2-automatic set
, which happens to be the set of numbers
whose binary representations contain at most two 1s: 1,
2, 3, 4, 5, 6, 8, 9, 10, 12, 16, 17, 18, ... (OEIS A048645).
Similarly,
is divisible by 9 unless
belongs to a 3-automatic set
, consisting of numbers
for which the representation of
in ternary consists entirely
of 0s and 2s (except possibly for a pair of adjacent 1s). The initial elements of
are 1, 2, 3, 4, 6, 7, 9, 10, 11, 12, 13, 18, 19, 21, 22, 27, ... (OEIS A051382).
If
is squarefree, then
must belong to
. It is very probable that
is finite, but no proof is known. Now, squares larger than
4 and 9 might also divide
, but by eliminating these two alone, the only possible
for
are 1, 2, 3, 4, 6, 9, 10, 12, 18, 33, 34, 36, 40, 64, 66, 192, 256, 264, 272, 513,
514, 516, 576 768, 1026, 1056, 2304, 16392, 65664, 81920, 532480, and 545259520.
All of these but the last have been checked, establishing that there are no other
such that
is squarefree for
.
Erdős showed that the binomial coefficient with
is a power of an integer for the single case
(Le Lionnais 1983, p. 48). Binomial coefficients
are squares
when
is a triangular number, which occur for
, 6, 35, 204, 1189, 6930, ... (OEIS
A001109). These values of
have the corresponding values
, 9, 50, 289, 1682, 9801, ... (OEIS A052436).
The binomial coefficients are called central
binomial coefficients, where
is the floor function,
although the subset of coefficients
is sometimes also given this name. Erdős and Graham
(1980, p. 71) conjectured that the central
binomial coefficient
is never squarefree
for
,
and this is sometimes known as the Erdős
squarefree conjecture. Sárkőzy's
theorem (Sárkőzy 1985) provides a partial solution which states that
the binomial coefficient
is never squarefree for
all sufficiently large
(Vardi 1991). Granville and Ramare (1996) proved that
the only squarefree values are
and 4. Sander (1992) subsequently showed that
are also never squarefree
for sufficiently large
as long as
is not "too big."
For ,
,
and
distinct primes, then the function (◇) satisfies
|
(18)
|
(Vardi 1991, p. 66).
Most binomial coefficients with
have a prime factor
, and Lacampagne et al. (1993) conjecture that
this inequality is true for all
, or more strongly that any such binomial coefficient
has least prime factor
or
with the exceptions
,
,
,
for which
, 19, 23, 29 (Guy 1994, p. 84).
The binomial coefficient (mod 2) can be computed using the XOR
operation
XOR
,
making Pascal's triangle mod 2 very easy to construct.
Sondow (2005) and Sondow and Zudilin (2006) noted the inequality
|
(19)
|
for
a positive integer and
a real number.