The truncated dodecahedron is the 32-faced Archimedean solid with faces . It is also uniform
polyhedron with Maeder index 26 (Maeder 1997), Wenninger index 10 (Wenninger
1989), Coxeter index 29 (Coxeter et al. 1954), and Har'El index 31 (Har'El
1993). It has Schläfli symbol t
and Wythoff symbol
. It is illustrated above together
with a wireframe version and a net that can be used for its
construction.
Some symmetric projections of the truncated dodecahedron are illustrated above.
It is implemented in the Wolfram Language as UniformPolyhedron["TruncatedDodecahedron"] or PolyhedronData["TruncatedDodecahedron"].
The truncated dodecahedron is the convex hull of the great ditrigonal dodecicosidodecahedron, great dodecicosahedron, and great icosicosidodecahedron uniform polyhedra.
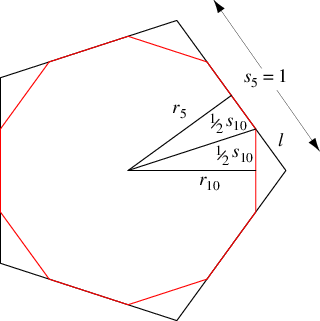
To construct the truncated dodecahedron by truncation, note that we want the inradius of the truncated pentagon to correspond with that of
the original pentagon,
, of unit side length
. This means that the side lengths
of the decagonal faces in the truncated dodecahedron
satisfy
|
(1)
|
giving
|
(2)
|
The length of the corner which is chopped off is therefore given by
|
(3)
|
The dual polyhedron of the truncated dodecahedron is the triakis icosahedron, both of which
are illustrated above together with their common midsphere.
The inradius of the dual, midradius
of the solid and dual, and circumradius
of the solid for
are
|
(4)
| |||
|
(5)
| |||
|
(6)
|
The distances from the center of the solid to the centroids of the triangular and decagonal faces are given by
|
(7)
| |||
|
(8)
|
The surface area and volume are
|
(9)
| |||
|
(10)
|
The unit truncated dodecahedron has Dehn invariant
|
(11)
| |||
|
(12)
| |||
|
(13)
|
(OEIS A377698), where the first expression uses the basis of Conway et al. (1999).
