The (semiregular) triakis icosahedron is the dual polyhedron of the truncated dodecahedron (Holden 1971, p. 55). It has 60 faces and is illustrated above together with a wireframe version and a net that can be used for its construction.
Note that Wenninger (1989, p. 46) uses the term "triakis octahedron" to refer to the small triambic icosahedron.
The triakis icosahedron is Wenninger dual 
.
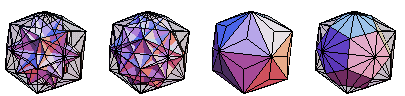
A tetrahedron 10-compound, cube 5-compound, icosahedron, and dodecahedron can be inscribed on the vertices of the triakis icosahedron (E. Weisstein, Dec. 25-27, 2009).
Taking the dual of a truncated dodecahedron with unit edge lengths gives a triakis icosahedron with edge lengths
 |  |  |
(1)
|
 |  |  |
(2)
|
The surface area and volume are
 |  |  |
(3)
|
 |  |  |
(4)
|
