A number of attractive tetrahedron 10-compounds can be constructed. The first (left figures) can be obtained by combining tetrahedron 5-compounds of opposite chirality combined.
The vertices of the first tetrahedron 10-compound are among the vertices of the dodecahedron-icosahedron compound and great stellated dodecahedron.
The tetrahedron 10-compounds illustrated above are implemented in the Wolfram Language as PolyhedronData["TetrahedronTenCompound",
n
]
for
and 2.
These tetrahedron 10-compounds are illustrated above together with their duals and common midspheres.
The common solids and convex hulls are illustrated above. For the first compound, the interior is a regular icosahedron and the convex hull is a regular dodecahedron. For the second, the interior is a square-augmented cuboctahedron and the convex hull is a chamfered cube.
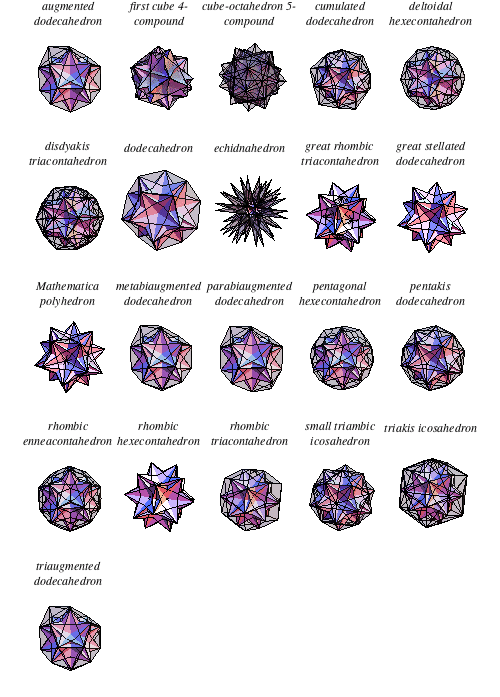
The tetrahedron 10-compound can be inscribed in the vertices of an augmented dodecahedron, (first) cube 4-compound, cube-octahedron 5-compound, augmented dodecahedron, deltoidal hexecontahedron, disdyakis triacontahedron, dodecahedron, echidnahedron, great rhombic triacontahedron, great stellated dodecahedron, metabiaugmented dodecahedron, parabiaugmented dodecahedron, pentagonal hexecontahedron, pentakis dodecahedron, rhombic enneacontahedron, rhombic hexecontahedron, rhombic triacontahedron, small triambic icosahedron, spikey, triakis icosahedron, and triaugmented dodecahedron (E. Weisstein, Dec. 25-28, 2009).