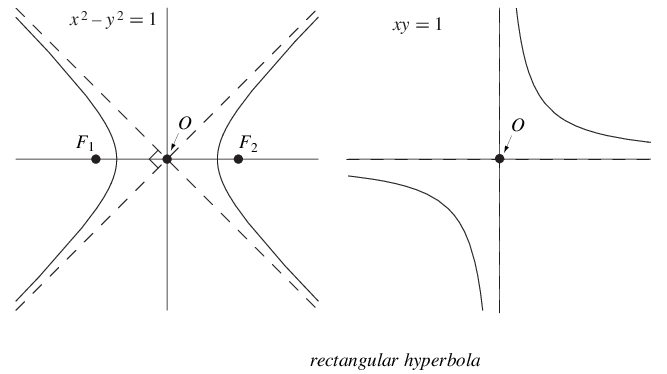
A hyperbola for which the asymptotes are perpendicular, also called an equilateral hyperbola
or right hyperbola. This occurs when the semimajor
and semiminor axes are equal. This corresponds
to taking ,
giving eccentricity
. Plugging
into the general equation of a hyperbola
with semimajor axis parallel to the x-axis
and semiminor axis parallel to the y-axis
(i.e., vertical conic section directrix),
|
(1)
|
therefore gives
|
(2)
|
The rectangular hyperbola opening to the left and right has polar equation
|
(3)
|
and the rectangular hyperbola opening in the first and third quadrants has the Cartesian equation
|
(4)
|
The parametric equations for the right branch of a rectangular hyperbola are given by
|
(5)
| |||
|
(6)
|
where
is the hyperbolic cosine and
is the hyperbolic sine.
The curvature, arc length,
and tangential angle for the above parametrization
with
are
|
(7)
| |||
|
(8)
| |||
![asqrt(cosh(2t))+([Gamma(3/4)]^2)/(sqrt(2pi))-sqrt(2)e^(-t)_2F_1(-1/4,1/2;3/4;-e^(4t))](/images/equations/RectangularHyperbola/Inline21.svg) |
(9)
| ||
![asqrt(cosh(2t))+([Gamma(3/4)]^2)/(sqrt(2pi))+1/4(i+1)B(-e^(4t);-1/4,1/2)](/images/equations/RectangularHyperbola/Inline24.svg) |
(10)
| ||
|
(11)
|
where
is an elliptic integral of the second
kind,
is the gamma function,
is a hypergeometric
function,
is an incomplete beta function, and
is a hyperbolic
tangent.
A parametrization which gives both branches is given by
|
(12)
| |||
|
(13)
|
with
and discontinuities at
.
The inverse curve of a rectangular hyperbola with inversion center at the center of the hyperbola is a lemniscate (Wells 1991).

If the three vertices of a triangle lie on a rectangular hyperbola, then so does the orthocenter
(Wells 1991). Equivalently, if four points form an orthocentric
system, then there is a family of rectangular hyperbolas through the points.
Moreover, the locus of centers
of these hyperbolas is the nine-point
circle of the triangle (Wells 1991).
If four points do not form an orthocentric system, then there is a unique rectangular hyperbola passing through them, and its center is given by the intersection of the nine-point circles of the points taken three at a time (Wells 1991).