For every dimension , the orthogonal group
is the group of
orthogonal matrices.
These matrices form a group because they are closed
under multiplication and taking inverses.
Thinking of a matrix as given by coordinate functions, the set of matrices is identified
with
.
The orthogonal matrices are the solutions to the
equations
|
(1)
|
where
is the identity matrix, which are redundant. Only
of these are independent, leaving
"free variables." In
fact, the orthogonal group is a smooth
-dimensional submanifold.
Because the orthogonal group is a group and a manifold, it is a Lie group.
has a submanifold tangent space at the
identity that is the Lie algebra of antisymmetric
matrices
.
In fact, the orthogonal group is a compact Lie group.
The determinant of an orthogonal matrix is either 1 or , and so the orthogonal group has two components.
The component containing the identity is the special
orthogonal group
.
For example, the group
has group action on the
plane that is a rotation:
|
(2)
|
where
is any real number in
.
These matrices preserve the quadratic form
, and so they also preserve circles
, which are the group
orbits.
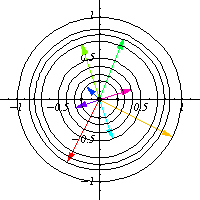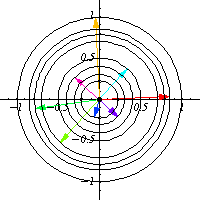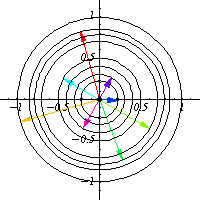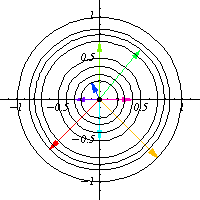
As a manifold,
consists of two disjoint copies of the circle.
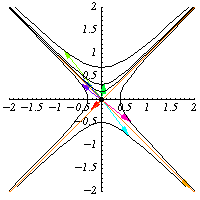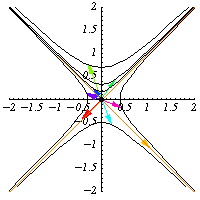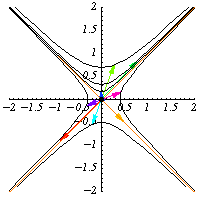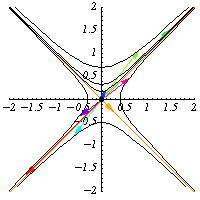
There are several generalizations of the orthogonal group. First, it is possible to define the orthogonal group for any symmetric quadratic form with matrix signature
. The group of matrices
which preserve
, that is,
|
(3)
|
is denoted .
The Lorentz group is
. For example, the matrices
|
(4)
|
are elements of .
They preserve the quadratic form
so they preserve the hyperbolas
.
Instead of using real numbers for the coefficients, it is possible to use coefficients from any field , in which case it is denoted
. The orthogonal matrices still satisfy
. For example,
contains
|
(5)
|
and has 48 elements in total.
Of course,
denotes the group of matrices which preserve the symmetric quadratic form of matrix
signature
,
with coefficients in the field
. When
is not
or
, these are called Lie-type groups.
When the coefficients are complex numbers, it is called the complex orthogonal group, which is much different from the unitary group. For example, matrices of the form
|
(6)
|
are in .
In particular,
is not a compact Lie group. The equations defining
in affine
space are polynomials of degree two. Consequently,
is a linear algebraic
group.
The numbers of subgroups of orders
, 2, 3, ... in the orthogonal group
are 1, 3, 1, 5, 1, 5, 1, 7, 1, 5, 1, 8, ... (OEIS A001051),
i.e., a repeating sequence of copies of
with the exceptions
,
,
,
, and
.