|
|
Let three similar isosceles triangles ,
, and
be constructed on the sides of a triangle
. Then
and
are perspective
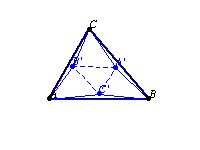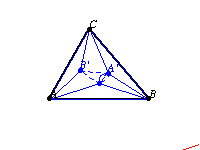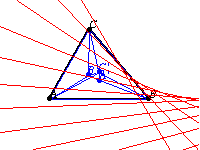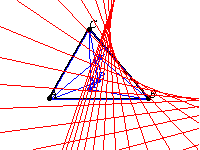
triangles, and the envelope of their perspectrix
as the vertex angle of the erected triangles is varied is a parabola
known as the Kiepert parabola. It has trilinear conic function
This parabola was first studied by Artzt (1884; Eddy and Fritsch 1994).
The Euler line of a triangle is the conic section directrix of the Kiepert parabola. In fact, the directrices
of all parabolas inscribed in a triangle pass through
the orthocenter. The Brianchon
point for the Kiepert parabola is the Steiner point of the reference
triangle, and the triangle
formed by the points of contact is called the
Steiner triangle.
The Kiepert parabola is tangent to the sides of the triangle (or their extensions), the line at infinity, and the Lemoine axis. The focus of the parabola has triangle center function
and is Kimberling center .
The Kiepert parabola passes through Kimberling centers for
(the isogonal conjugate
of the focus of the Kiepert parabola
), 669 (the crossdifference
of
and
,
1649, and 2528 (Weisstein, Oct. 16 and Dec. 13, 2004).
The polar triangle of the Kiepert parabola is the Steiner triangle.
The Kiepert parabola focus and Parry point are the two intersections of a triangle's circumcircle with its Parry circle.
is also the Feuerbach
point of the tangential triangle of
.