The unique (modulo rotations) scalene triangle formed from three vertices of a regular heptagon, having
vertex angles ,
,
and
.
There are a number of amazing formulas connecting the sides and angles of the heptagonal
triangle (Bankoff and Garfunkel 1973).
|
(1)
|
where
is the triangle's circumradius. The sum of squares
of sides of the heptagonal triangle is equal to
(Bankoff and Garfunkel 1973). The ratio
of inradius
to circumradius
is given by the positive root of
|
(2)
|
The side lengths satisfy
|
(3)
|
(Bankoff and Garfunkel 1973) and
|
(4)
|
The latter can be easily proved by applying Ptolemy's theorem to the quadrilateral with sides ,
,
, and
, and diagonals
and
, and dividing by
(I. Larrosa Cañestro, pers. comm., Apr. 23,
2006).
The Brocard angle satisfies
|
(5)
|
and the exradius is equal to the radius of the nine-point
circle of
.
is half the harmonic mean of the other two sides,
|
(6)
|
|
(7)
|
and so on for all permutations of variables (Bankoff and Garfunkel 1973). Also,
|
(8)
|
If ,
,
and
are the altitudes, then
|
(9)
|
|
(10)
|
If ,
,
and
are the feet of the altitudes, then
|
(11)
|
and so on (Bankoff and Garfunkel 1973). The internal angle bisectors of and
are equal to the difference of the adjacent sides and the
external angle bisector of
is equal to the sum of adjacent sides.
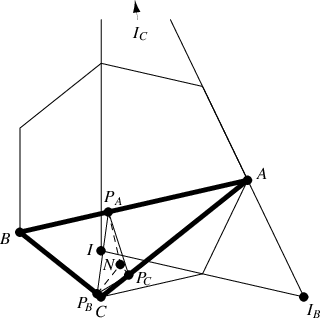
The triangle
joining the feet of the angle bisectors of the heptagonal triangle is an isosceles
triangle with
.
|
|
|
The orthic triangle and median triangle
are congruent and perspective.
In addition, both are similar to
, to the pedal triangle
of
with respect to the nine-point
center
,
and to the triangle
formed by the incenter
and the exterior angle bisectors
and
(Bankoff and Garfunkel 1973). The triangle
is also similar to these triangles.
There are also a slew of curious trigonometric identities involving the angles of the heptagonal triangle:
|
(12)
| |
|
(13)
| |
|
(14)
| |
|
(15)
| |
|
(16)
| |
|
(17)
| |
|
(18)
| |
|
(19)
| |
|
(20)
| |
|
(21)
| |
|
(22)
| |
|
(23)
| |
|
(24)
| |
|
(25)
| |
|
(26)
| |
|
(27)
| |
|
(28)
| |
|
(29)
| |
|
(30)
|
(Bankoff and Garfunkel 1973).
In addition,
|
(31)
|
Finally, the heptagonal triangle satisfies the miscellaneous properties:
1. The first Brocard point corresponds to the nine-point center and the second Brocard point lies on the nine-point circle.
2. ,
where
is the circumcenter,
is the orthocenter, and
is the circumradius.
3. ,
where
is the incenter and
is the inradius.
4. The two tangents from the orthocenter to the circumcircle of the
heptagonal triangle are mutually perpendicular.
5. The center of the circumcircle of the tangential triangle corresponds with the symmetric point of with respect to
.
6. The altitude from is half the length of the internal bisector of the angle
.