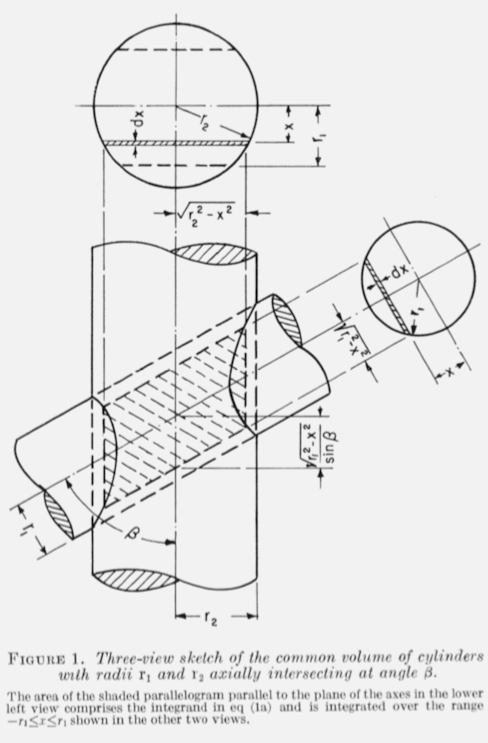
Consider two cylinders as illustrated above (Hubbell 1965) where the cylinders have radii
and
with
,
the larger cylinder is oriented along the
-axis, and where the axes of the two cylinders intersecting
at an angle
. Then the volume of the region of intersection is given
by
|
(1)
| |||
|
(2)
| |||
|
(3)
| |||
|
(4)
| |||
 |
(5)
|
where
|
(6)
|
Here,
and
are complete elliptic integrals
of the first and second
kinds, respectively,
is a hypergeometric
function, and
is a binomial coefficient.
The intersection of two (or three) right cylinders of equal radii intersecting at right angles is known as the Steinmetz solid.