A polynomial given by
 |
(1)
|
where
are the roots of unity in
given by
|
(2)
|
and
runs over integers relatively prime to
. The prime may be dropped if the product is instead taken
over primitive roots of unity, so that
 |
(3)
|
The notation
is also frequently encountered. Dickson et al. (1923) and Apostol (1975) give
extensive bibliographies for cyclotomic polynomials.
The cyclotomic polynomial for can also be defined as
|
(4)
|
where
is the Möbius function and the product is
taken over the divisors
of
(Vardi 1991, p. 225).
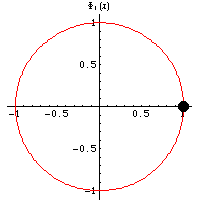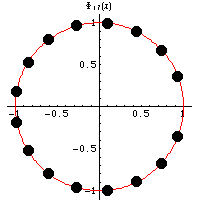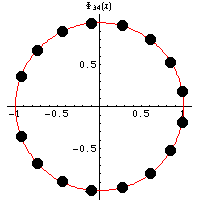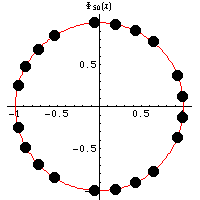
is an integer polynomial and an irreducible
polynomial with polynomial degree
, where
is the totient function.
Cyclotomic polynomials are returned by the Wolfram
Language command Cyclotomic[n,
x]. The roots of cyclotomic polynomials lie on the unit
circle in the complex plane, as illustrated
above for the first few cyclotomic polynomials.
The first few cyclotomic polynomials are
|
(5)
| |||
|
(6)
| |||
|
(7)
| |||
|
(8)
| |||
|
(9)
| |||
|
(10)
| |||
|
(11)
| |||
|
(12)
| |||
|
(13)
| |||
|
(14)
|
The cyclotomic polynomial is illustrated above in the complex
plane.
On any line through the origin, the value of a cyclotomic polynomial is strictly increasing outside the unit disk.
If
is an odd prime, then
|
(15)
| |||
|
(16)
| |||
|
(17)
| |||
|
(18)
| |||
|
(19)
| |||
|
(20)
|
(Riesel 1994, p. 306). Similarly, for again an odd prime,
|
(21)
| |||
|
(22)
| |||
|
(23)
|
For the first few remaining values of ,
|
(24)
| |||
|
(25)
| |||
|
(26)
| |||
|
(27)
| |||
|
(28)
| |||
|
(29)
| |||
|
(30)
| |||
|
(31)
|
(Riesel 1994, p. 307).
For
a prime relatively prime to
,
|
(32)
|
but if ,
|
(33)
|
(Nagell 1951, p. 160).
An explicit equation for for squarefree
is given by
 |
(34)
|
where
is the totient function and
is calculated using the recurrence
relation
 |
(35)
|
with ,
where
is the Möbius function and
is the greatest
common divisor of
and
.
The polynomial can be factored as
|
(36)
|
Furthermore,
|
(37)
| |||
|
(38)
|
The coefficients of the inverse of the cyclotomic polynomial
|
(39)
| |||
|
(40)
|
can also be computed from
|
(41)
| |||
|
(42)
| |||
|
(43)
|
where
is the floor function.
For prime,
 |
(44)
|
i.e., the coefficients are all 1. The first cyclotomic polynomial to have a coefficient other than
and 0 is
,
which has coefficients of
for
and
. This is true because 105 is the first number to have
three distinct odd prime factors, i.e.,
(McClellan and Rader 1979, Schroeder 1997).
The smallest values of
for which
has one or more coefficients
,
,
, ... are 0, 105, 385, 1365, 1785, 2805, 3135, 6545, 6545,
10465, 10465, 10465, 10465, 10465, 11305, ... (OEIS A013594).
It appears to be true that, for , if
factors, then the factors contain a cyclotomic
polynomial. For example,
|
(45)
| |||
|
(46)
|
This observation has been checked up to (Nicol 2000). If
and
are prime, then
is irreducible.
Migotti (1883) showed that coefficients of for
and
distinct primes can be only
0,
.
Lam and Leung (1996) considered
 |
(47)
|
for prime. Write the totient
function as
|
(48)
|
and let
|
(49)
|
then
1. iff
for some
and
,
2. iff
for
and
,
3. otherwise .
The number of terms having is
, and the number of terms having
is
. Furthermore, assume
, then the middle coefficient
of
is
.
Resultants of cyclotomic polynomials have been computed by Lehmer (1936), Diederichsen (1940), and Apostol (1970). It is known that if
, i.e.,
and
are relatively prime (Apostol 1975). Apostol (1975) showed
that for positive integers
and
and arbitrary nonzero complex numbers
and
,
![rho(Phi_m(ax),Phi_n(bx))=b^(phi(m)phi(n))product_(d|n)[Phi_(m/delta)((a^d)/(b^d))]^(mu(n/d)phi(m)/phi(m/delta)),](/images/equations/CyclotomicPolynomial/NumberedEquation14.svg) |
(50)
|
where
is the greatest common divisor of
and
,
is the totient function,
is the Möbius function,
and the product is over the divisors of
. If
and
are distinct primes
and
, then (50) simplifies to
 |
(51)
|
The following table gives the resultants ,
(OEIS A054372).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0 | ||||||
| 2 | 2 | 0 | |||||
| 3 | 3 | 1 | 0 | ||||
| 4 | 2 | 2 | 1 | 0 | |||
| 5 | 5 | 1 | 1 | 1 | 0 | ||
| 6 | 1 | 3 | 4 | 1 | 1 | 0 | |
| 7 | 7 | 1 | 1 | 1 | 1 | 1 | 0 |
The numbers of 1s in successive rows of this table are given by 0, 0, 1, 1, 3, 3, 5, 4, 6, 7, 9, ... (OEIS A075795).
The cyclotomic polynomial has the particularly nice Maclaurin
series
|
(52)
|
whose coefficients 1, 0, ,
, 0, 1, 1, 0,
,
, ... (OEIS A010892)
are given by solving the recurrence equation
|
(53)
|
with
(Wolfram 2002, p. 128),
giving the explicit form
|
(54)
|
Interestingly, any sequence satisfying the linear
recurrence equation
|
(55)
|
can be written as
|
(56)
|