The simple continued fraction representations for Catalan's constant is [0, 1, 10, 1, 8, 1, 88, 4, 1, 1, ...] (OEIS A014538).
A plot of the first 256 terms of the continued fraction represented as a sequence
of binary bits is shown above.
Record computations are summarized below.
| terms | date | by |
| Jul. 20, 2013 | E. Weisstein | |
| Aug. 7, 2013 | E. Weisstein |
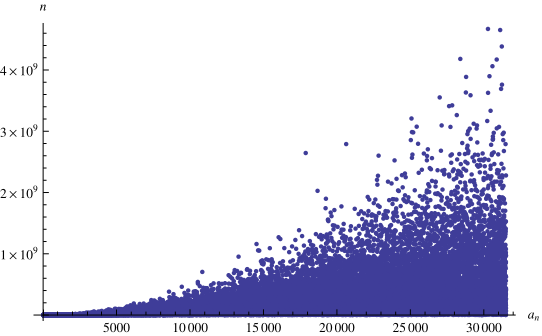
The plot above shows the positions of the first occurrences of 1, 2, 3, ... in the continued fraction, the first few of which are 1, 13, 14, 7, 45, 36, 10, 4, 21, 2,
... (OEIS A196461; illustrated above). The
smallest number not occurring in the first terms of the continued fraction are 31516, 31591,
32600, 32806, 33410, ... (E. Weisstein, Aug. 8, 2013).
The cumulative largest terms in the continued fraction are 0, 1, 10, 88, 322, 330, 1102, 6328, ... (OEIS A099789), which occur at positions 0, 1, 2, 6, 105, 284, 747, 984, 2230, 5377, ... (OEIS A099790).
Let the continued fraction of be denoted
and let the denominators of the convergents
be denoted
,
, ...,
. Then plots above show successive values of
,
,
, which appear to converge to Khinchin's
constant (left figure) and
, which appear to converge to the Lévy
constant (right figure), although neither of these limits has been rigorously
established.
The Engel expansion of is given by 2, 2, 2, 4, 4, 5, 5, 12, 13, 41, 110, ... (OEIS
A054543).