TOPICS
Search

e Continued Fraction

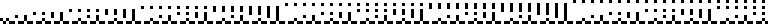
e continued fraction binary plot

The simple continued fraction representations of e given by [2; 1, 2, 1, 1, 4, 1, 1, 6, ...] (OEIS A003417). This continued fraction is sometimes known as Euler's continued fraction. A plot of the first 256 terms of the continued fraction represented as a sequence of binary bits is shown above.

The convergents can be given in closed form as ratios of confluent hypergeometric functions of the first kind (Komatsu 2007ab), with the first few being 2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, ... (OEIS A007676 and A007677). These are good to 0, 0, 1, 1, 2, 3, 3, 4, 5, 5, ... (OEIS A114539) decimal digits, respectively.

Other continued fraction representations are

(e-1)/(e+1)=[0;2,6,10,14,...]
(1)
e-1=[1;1,2,1,1,4,1,1,6,...]
(2)
1/2(e-1)=[0;1,6,10,14,...]
(3)

(Olds 1963, pp. 135-136). Amazingly, not only the continued fractions e, but those of rational powers of e show regularity, for example

e^(1/2)=[1,1,1,1,5,1,1,9,1,1,13,...]
(4)
e^(1/3)=[1,2,1,1,8,1,1,14,1,1,20,...]
(5)
e^(1/4)=[1,3,1,1,11,1,1,19,1,1,27,...]
(6)
e^(1/5)=[1,4,1,1,14,1,1,24,1,1,34,...].
(7)

A beautiful non-simple continued fraction for e is given by

e=2+1/(1+1/(2+2/(3+3/...)))
(8)

(Wall 1948, p. 348).

EKhinchinLevy

Let the continued fraction of e be denoted [a_0;a_1,a_2,...] and let the denominators of the convergents be denoted q_1, q_2, ..., q_n. Then plots above show successive values of a_1^(1/1), (a_1a_2)^(1/2), ..., (a_1a_2...a_n)^(1/n) (left figure) and q_n^(1/n) (right figure). As can be seen from the plots, the regularity in the continued fraction of e means that e is one of a set of numbers of measure 0 whose continued fraction sequences do not converge to Khinchin's constant or the Lévy constant.

e has a very regular Engel expansion, namely 1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... (OEIS A000027).

See also

e, e Digits, Euler's Continued Fraction

Explore with Wolfram|Alpha

References

Cohn, H. "A Short Proof of the Simple Continued Fraction Expansion of e." Amer. Math. Monthly 113, 57-62, 2006.Komatsu, T. "Some Combinatorial Properties of the Leaping Convergents." Integers: Elec. J. Combin. Num. Th. 7, 1-10, 2007a.Komatsu, T. "Some Combinatorial Properties of the Leaping Convergents." In Proceedings of the Integers Conference 2005 in celebration of the 70th birthday of Ronald Graham held at the University of West Georgia, Carrollton, GA, October 27-30, 2005 (Ed. B. Landman, M. B. Nathanson, J. Nesetril, R. J. Nowakowski, and C. Pomerance). Berlin: de Gruyter, pp. 315-325, 2007b.Olds, C. D. Continued Fractions. New York: Random House, 1963.Olds, C. D. "The Simple Continued Fraction Expression of e." Amer. Math. Monthly 77, 968-974, 1970.Sloane, N. J. A. Sequences A000027/M0472, A003417/M0088, A007676/M0869, A007677/M2343, and A114539 in "The On-Line Encyclopedia of Integer Sequences."Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.

Cite this as:

Weisstein, Eric W. "e Continued Fraction." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/eContinuedFraction.html

Subject classifications