Let be a finite-dimensional split semisimple
Lie algebra over a field of field
characteristic 0,
a splitting Cartan subalgebra, and
a weight of
in a representation of
. Then
is also a weight. Furthermore, the reflections with
a root, generate a group of linear transformations in
called the Weyl group
of
relative to
,
where
is the algebraic
conjugate space of
and
is the Q-space
spanned by the roots (Jacobson 1979, pp. 112, 117, and 119).
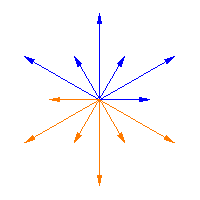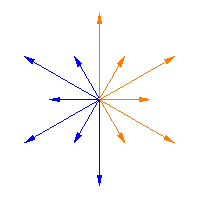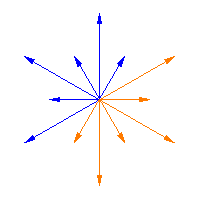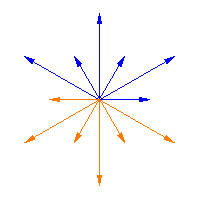
|
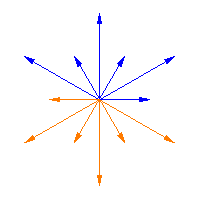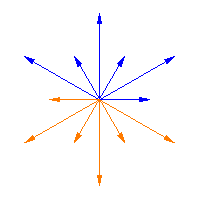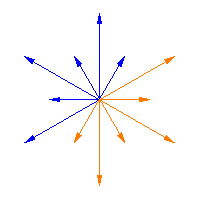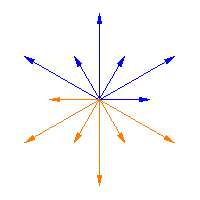
|
|
The Weyl group acts on the roots of a semisimple Lie algebra, and it is a finite group. The animations above illustrate this action for Weyl Group acting on the roots
of a homotopy from one Weyl matrix to the next one (i.e., it slides the arrows from
to
) in the first two figures, while the third figure shows the
Weyl Group acting on the roots of the Cartan matrix
of the infinite family of semisimple lie algebras
(cf. Dynkin diagram),
which is the special linear Lie algebra,
.