A schematic diagram used in logic theory to depict collections of sets and represent their relationships.
The Venn diagrams on two and three sets are illustrated above. The order-two diagram (left) consists of two intersecting circles, producing
a total of four regions, ,
,
, and
(the empty set, represented
by none of the regions occupied). Here,
denotes the intersection
of sets
and
.
The order-three diagram (right) consists of three symmetrically placed mutually intersecting circles comprising
a total of eight regions. The regions labeled ,
,
and
consist of members which are only in
one set and no others, the three regions labelled
,
, and
consist of members which are in two sets but
not the third, the region
consists of members which are simultaneously in all three, and no regions occupied
represents
.
In general, an order-
Venn diagram is a collection of
simple closed curves in the plane
such that
1. The curves partition the plane into connected regions, and
2. Each subset of
corresponds to a unique region formed by the intersection of the interiors of the
curves in
(Ruskey).
Since there are
(the binomial coefficient) ways to pick
members from a total of
, the number of regions in an order
Venn diagram is
 |
(where the region outside the diagram is included in the count).
The region of intersection of the three circles in the
order three Venn diagram in the special case of the center of each being located
at the intersection of the other two is a geometric
shape known as a Reuleaux triangle.
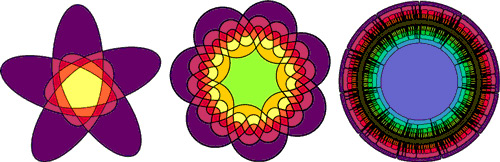
The left figure at left above shows an Venn diagram due to Branko Grünbaum, while the attractive
7-fold rosette illustrated in the middle figure is an
Venn diagram called "Victoria" by Ruskey. The
right figure shows a recently constructed symmetric Venn diagram on
due to Ruskey, Carla Savage, and Stan Wagon.
In Season 4 episode "Power" of the television crime drama NUMB3RS, mathematical genius Charles Eppes constructs a Venn diagram to determine suspects who match a particular description and have a history of violence.