TOPICS
Search

Vector Field

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
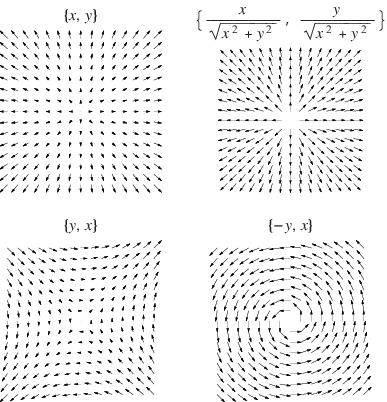
VectorPlot

A vector field is a map f:R^n|->R^n that assigns each x a vector f(x). Several vector fields are illustrated above. A vector field is uniquely specified by giving its divergence and curl within a region and its normal component over the boundary, a result known as Helmholtz's theorem (Arfken 1985, p. 79).

Vector fields can be plotted in the Wolfram Language using VectorPlot[f, {x, xmin, xmax}, {y, ymin, ymax}].

Flows are generated by vector fields and vice versa. A vector field is a tangent bundle section of its tangent bundle.

See also

Flow, Newtonian Vector Field, Pólya Plot, Scalar Field, Seifert Conjecture, Slope Field, Tangent Bundle, Vector, Wilson Plug Explore this topic in the MathWorld classroom

Explore with Wolfram|Alpha

References

Arfken, G. "Vector Analysis." Ch. 1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 1-84, 1985.Gray, A. "Vector Fields on R^n" and "Derivatives of Vector Fields on R^n." §11.4 and 11.5 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 255-258, 1997.Morse, P. M. and Feshbach, H. "Vector Fields." §1.2 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 8-21, 1953.

Referenced on Wolfram|Alpha

Vector Field

Cite this as:

Weisstein, Eric W. "Vector Field." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/VectorField.html

Subject classifications