Turmites, also called turning machines, are 2-dimensional Turing machines in which the "tape" consists of a grid of spaces that can be written and erased by an active ("head") element that turns at each iteration on the basis of the state of its current grid square. The "head" of the system is usually called a "vant," "ant," or "turmite" on square grids, and a "bee," "worm," or "turtle" on hexagonal grids. (The term "turtle" is named after Seymour Papert's turtle geometry). The turmite tracks its position, direction, and current state.
|
|
|
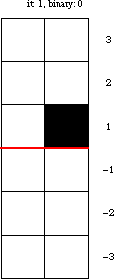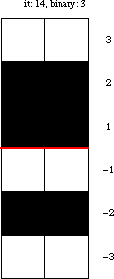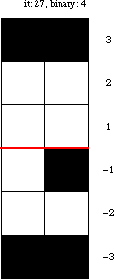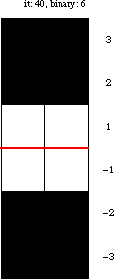
Amazingly, the turmite with rule illustrated above mimics binary counting. In this turmite, the pattern of bands above the red line corresponds to incrementing binary digits. After each cycle constructing the upper pattern, the same pattern is produced (mirrored left-to-right) below the red line.
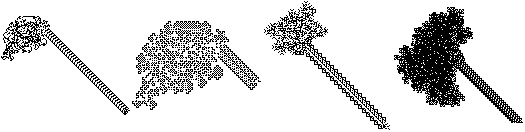
The figures above show a sample of turmites that build structures which travel down and to the right called "highways" (top figures) together with their underlying rules (bottom figures). The turmites on the left is known as Langton's ant and is the most famous turmite. The second turmite shows a 2-state 2-color rule that is essentially equivalent to Langton's ant. In this rule, if the state is 1 and the underlying cell is gray, the cell is changed to white, the state is changed to 2, and the turmite turns left.

Highways with other possible orientations are illustrated above. In the third image, the highway gets thicker as it lengthens.
Growth around the edges is frequently seen. The fourth image illustrates a turmite which will grow even within a field of sparse random data.

Spirals are quite common. The second turmite above constructs a golden rectangle.


Chaotic behavior of many different types can happen. For example, the fourth turmite in the first row displays a behavior in which it counts incrementally.

In addition to persistent structures, nested growth, and chaotic behavior, it is possible for the turmite to cycle in a loop of arbitrary size. No procedure is known for determining whether this ever happens for a general turmite. The illustration above shows a turmite that gets trapped in a cycle after some amount of growth.