Two submanifolds and
in an ambient space
intersect transversally if,
for all
,
where the addition is in , and
denotes the tangent map
of
.
If two submanifolds do not intersect, then they
are automatically transversal. For example, two curves in
are transversal only if they do not intersect
at all. When
and
meet transversally then
is a smooth submanifold
of the expected dimension
.
In some sense, two submanifolds "ought" to intersect transversally and, by Sard's theorem, any intersection can be perturbed to be transversal. Intersection in homology only makes sense because an intersection can be made to be transversal.
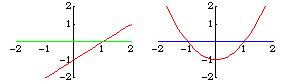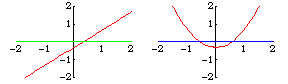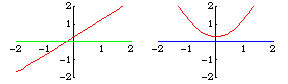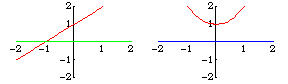
Transversality is a sufficient condition for an intersection to be stable after a perturbation. For example, the lines and
intersect transversally,
as do the perturbed lines
, and they intersect at
only one point. However,
does not intersect
transversally. It intersects in one point, while
intersects in either none or two points, depending
on whether
is positive or negative.
When ,
then a transversal intersection is an isolated point.
If the three spaces have an vector space orientation,
then the transversal condition means it is possible to assign a sign to the intersection.
If
are an oriented basis for
and
are an oriented basis for
, then the intersection is
if
is oriented in
and
otherwise.
More generally, two smooth maps and
are transversal if whenever
then
.