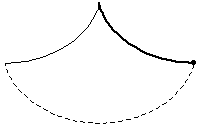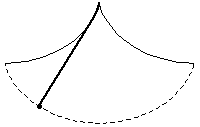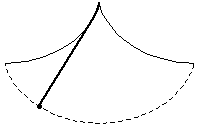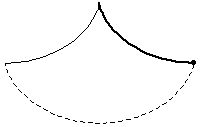
The problem of finding the curve down which a bead placed anywhere will fall to the bottom in the same amount of time. The solution is a cycloid, a fact first discovered and published by Huygens in Horologium oscillatorium (1673). This property was also alluded to in the following passage from Moby Dick: "[The try-pot] is also a place for profound mathematical meditation. It was in the left-hand try-pot of the Pequod, with the soapstone diligently circling round me, that I was first indirectly struck by the remarkable fact, that in geometry all bodies gliding along a cycloid, my soapstone, for example, will descend from any point in precisely the same time" (Melville 1851).
Huygens also constructed the first pendulum clock with a device to ensure that the pendulum was isochronous by forcing the pendulum to swing in an arc of a cycloid. This is accomplished by placing two evolutes of inverted cycloid arcs on each side of the pendulum's point of suspension against which the pendulum is constrained to move (Wells 1991, p. 47; Gray 1997, p. 123). Unfortunately, friction along the arcs causes a greater error than that corrected by the cycloidal path (Gardner 1984).
The parametric equations of the cycloid are
|
(1)
| |||
|
(2)
|
To see that the cycloid satisfies the tautochrone property, consider the derivatives
|
(3)
| |||
|
(4)
|
and
|
(5)
| |||
|
(6)
|
Now
|
(7)
|
|
(8)
|
|
(9)
| |||
 |
(10)
| ||
 |
(11)
| ||
 |
(12)
|
so the time required to travel from the top of the cycloid to the bottom is
 |
(13)
|
However, from an intermediate point ,
|
(14)
|
so
 |
(15)
| ||
 |
(16)
|
To integrate, rearrange this equation using the half-angle formulas
 |
(17)
| ||
 |
(18)
|
with the latter rewritten in the form
|
(19)
|
to obtain
 |
(20)
|
Now transform variables to
 |
(21)
| ||
 |
(22)
|
so
 |
(23)
| ||
![2sqrt(a/g)[sin^(-1)u]_0^1](/images/equations/TautochroneProblem/Inline55.svg) |
(24)
| ||
 |
(25)
|
and the amount of time is the same from any point.