The Simson line is the line containing the feet ,
,
and
of the perpendiculars from an arbitrary
point
on the circumcircle
of a triangle to the sides or their extensions of the
triangle. This line was attributed to Simson by Poncelet,
but is now frequently known as the Wallace-Simson line since it does not actually
appear in any work of Simson (Johnson 1929, p. 137; Coxeter and Greitzer 1967,
p. 41; de Guzmán 1999). The inverse statement to that given above, namely
that the locus of all points
in the plane of a triangle
such that the feet of perpendiculars
from the three sides of the triangle is collinear is given by the circumcircle
of
, is sometimes called the Wallace-Simson
theorem (de Guzmán 1999).
The trilinear equation of the Simson line for a point lying on the circumcircle,
i.e., satisfying
is
 |
(P. Moses, pers. comm., Jan. 27, 2005).
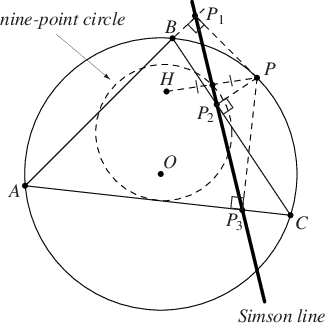
The Simson line bisects the line , where
is the orthocenter (Honsberger
1995, p. 46). Moreover, the midpoint of
lies on the nine-point circle
(Honsberger 1995, pp. 46-47). The Simson lines of two opposite point on the
circumcenter of a triangle are perpendicular
and meet on the nine-point circle.
The angle between the Simson lines of two points and
is half the angle of the arc
. The Simson line of any polygon
vertex is the altitude through that polygon
vertex. The Simson line of a point opposite a polygon
vertex is the corresponding side. If
is the Simson line of a point
of the circumcircle, then
the triangles
and
are directly similar.
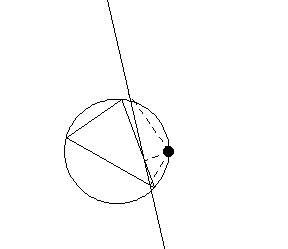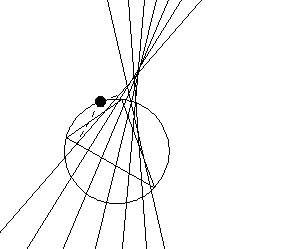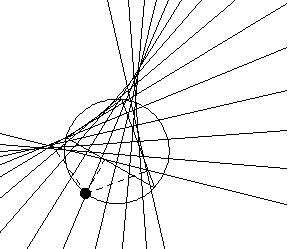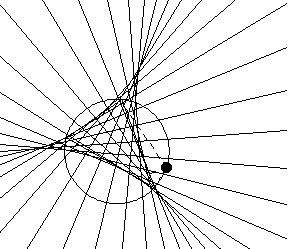
The envelope of the Simson lines of a triangle is a deltoid (Butchart 1939; Wells 1991, pp. 155 and
230). The area of the deltoid is half the area of the circumcircle (Wells 1991, p. 230),
and the first Morley triangle of the starting
triangle has the same orientation as the deltoid. Each
side of the triangle is tangent to the deltoid at a point
whose distance from the midpoint of the side equals
the chord of the nine-point circle cut off by
that side (Wells 1991, p. 231). If a line is the Simson line of a point
on the circumcircle of a
triangle, then
is called the Simson line pole
of
(Honsberger 1995, p. 128).
The altitudes of a reference triangle are Simson lines whose Simson line poles are the vertices of the reference triangle. Furthermore, the sides of the reference triangle are also Simson lines whose Simson line poles are the reflections of the vertices of the reference triangle about its circumcenter. Note also that the nontrivial perpendicular feet from these reflective vertices intersect the sides of the reference triangle at points that are the tangents to the Steiner deltoid.