Let the inner and outer Soddy triangles of a reference triangle be denoted
and
, respectively. Similarly, let the tangential
triangles of
and
be denoted
and
, respectively. Then the inner (respectively,
outer) Rigby point Ri (respectively,
) is the perspector of
and
(respectively,
and
) (Oldknow 1996). The Rigby points lie on the
Soddy line. They have triangle
center functions
|
(1)
| |||
|
(2)
|
which are Kimberling centers and
, respectively.
Honsberger (1995) defines a different point which he calls the "Rigby point" . Let
be an arbitrary chord of the circumcircle of a given triangle
, and let
be the Simson line pole
of the Simson line
with respect to
which is perpendicular
to
. Then it also turns out that
and
. In addition,
,
, and
with respect to
.
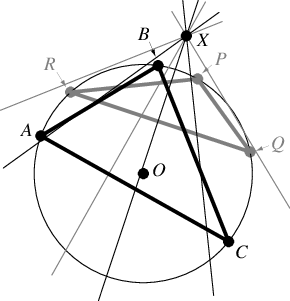
As a result of these remarkable facts, it can be shown that the Simson lines ,
, and
with respect to
meet in the Rigby point
. Moreover, the Simson lines
,
, and
with respect to
also meet in
, and
is the orthopole of
,
,
and
with respect to
, and of
,
,
and
with respect to
. Finally,
is the midpoint of the orthocenters
of
and
(Honsberger 1996, p. 136).