The sign of a real number, also called sgn or signum, is for a negative number (i.e.,
one with a minus sign "
"), 0 for the number zero, or
for a positive
number (i.e., one with a plus sign "
"). In other words, for real
,
 |
(1)
|
For real , this can be written
|
(2)
|
and satisfies
 |
(3)
|
for real
can also be defined as
|
(4)
|
where is the Heaviside
step function.
The sign function is implemented in the Wolfram Language for real
as Sign[x].
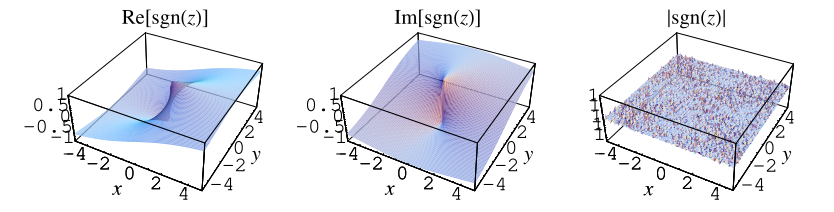
For nonzero complex numbers, Sign[z]
returns
, where
is the complex modulus
of
.
can also be interpreted as an unspecified
point on the unit circle in the complex plane (Rich and Jeffrey 1996).