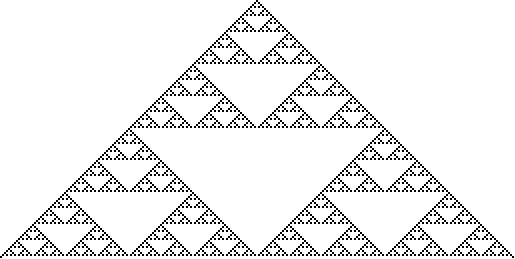
The Sierpiński sieve is a fractal described by Sierpiński in 1915 and appearing in Italian art from the 13th century (Wolfram 2002, p. 43).
It is also called the Sierpiński gasket or Sierpiński triangle. The curve
can be written as a Lindenmayer system with
initial string "FXF--FF--FF", string
rewriting rules "F" -> "FF", "X"
-> "--FXF++FXF++FXF--", and angle .
The th
iteration of the Sierpiński sieve is implemented in the Wolfram
Language as SierpinskiMesh[n].
Let
be the number of black triangles after iteration
,
the length of a side of a triangle, and
the fractional area which is black
after the
th
iteration. Then
|
(1)
| |||
|
(2)
| |||
|
(3)
|
The capacity dimension is therefore
|
(4)
| |||
|
(5)
| |||
|
(6)
| |||
|
(7)
|
(OEIS A020857; Wolfram 1984; Borwein and Bailey 2003, p. 46).
The Sierpiński sieve is produced by the beautiful recurrence equation
|
(8)
|
where
denote bitwise XOR. It is also given by
 |
(9)
|
where
is the
st
least significant bit defined by
 |
(10)
|
and the product is taken over all such that
(Allouche and Shallit 2003, p. 113).
The Sierpinski sieve is given by Pascal's triangle (mod 2), giving the sequence 1; 1, 1; 1, 0, 1; 1, 1, 1, 1; 1, 0, 0, 0, 1; ... (OEIS
A047999; left figure). In other words, coloring
all odd numbers black and even
numbers white in Pascal's triangle produces
a Sierpiński sieve (Guy 1990; Wolfram 2002, p. 870;
middle figure). The binomial coefficient mod 2 can be computed using bitwise
operations AND(NOT(
),
), giving the sequence 0; 0, 0; 0, 1,
0; 0, 0, 0, 0; 0, 1, 2, 3, 0; ... (OEIS A102037;
right figure), then coloring the triangle black if the result is 0 and white otherwise.
This is a consequence of the Lucas correspondence
theorem for binomial coefficients modulo a prime number.
Surprisingly, elementary cellular automaton rules 60, 90 and 102 (when omitting the trailing zeros) also produce the Sierpinski sieve (Wolfram 2002, p. 870). Wolfram (2002, pp. 931-932) gives a large number of algorithms that can be used to compute a Sierpiński sieve.
Gardner (1977) and independently Watkins (Conway and Guy 1996, Krížek et al. 2001) noticed that the number of sides for constructible polygons with odd Numbers of sides are given by the first 32 rows of the Sierpiński sieve interpreted as binary numbers, giving 1, 3, 5, 15, 17, 51, 85, 255, ... (OEIS A004729, Conway and Guy 1996, p. 140). In other words, every row is a product of distinct Fermat primes, with terms given by binary counting.