 |
is the trigonometric function defined
by
 |  |  |
(1)
|
 |  |  |
(2)
|
where 
is the cosine.
The secant is implemented in the Wolfram
Language as Sec[z].
Note that the secant does not appear to be in consistent widespread use in Europe, although it does appear explicitly in various German and Russian handbooks (e.g.,
Gradshteyn and Ryzhik 2000, p. 43). Interestingly, while 
is treated on a par with the other trigonometric functions
in some tabulations (Gellert et al. 1989, p. 222), it is not in others
(Gradshteyn and Ryzhik 2000, who do not list it in their table of "basic functional
relations" on p. 28, but do give identities involving it on p. 43).
Tropfke states, "The history of the secant function begins almost contemporaneously with that of the tangent, but ended after discovery of logarithmic calculation in the first half of the 17th century" (Tropfke 1923, pp. 28) and, "The secant naturally disappeared again from trigonometry when, after the introduction of logarithms, the appearance of trigonometric functions in the denominator no longer posed any difficulty" (Tropfke 1923, pp. 30). Harris and Stocker (1998, p. 300) call secant and cosecant "rarely used functions," but then devote an entire section to them. Because these functions do seem to be in widespread use in the United States (e.g., Abramowitz and Stegun 1972, p. 72), reports of their demise seem to be a bit premature.
The derivative is
 |
(3)
|
and the indefinite integral is
![intseczdz=ln[cos(1/2z)+sin(1/2z)]-ln[cos(1/2z)-sin(1/2z)]+C,](/images/equations/Secant/NumberedEquation2.svg) |
(4)
|
where 
is a constant
of integration. For 
,
this can be written
 |  | ![ln[tan(1/4pi+1/2z)]+C](/images/equations/Secant/Inline14.svg) |
(5)
|
 |  |  |
(6)
|
The Maclaurin series of the secant is
 |  |  |
(7)
|
 |  |  |
(8)
|
(OEIS A046976 and A046977), where 
is an Euler
number. The first few reduced numerators that are prime are 5, 61, 277, 23489580527043108252017828576198947741,
... (OEIS A092838), corresponding to 
, 3, 4, 19, 24, ... (OEIS A092837).
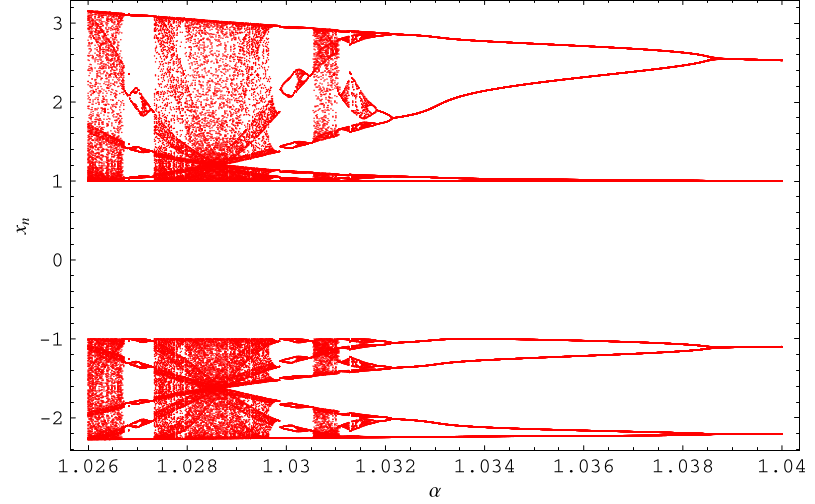
A bifurcation plot of 
is illustrated above (Trott 2004, p. 169). Of all the trigonometric functions,
is apparently the only one displaying
interesting bifurcation structure for iterates of this form.
The positive integer values of 
giving incrementally largest values of 
are given by 1, 2, 5, 8, 11, 344, 699, 1054, 1409, 1764,
2119, ... (OEIS A004112), corresponding to
the values 1.85082, 2.403, 3.52532, 6.87285, 225.953, 227.503, ....
and Cosecant 
Functions." Ch. 33 in