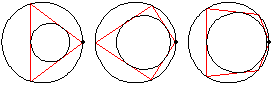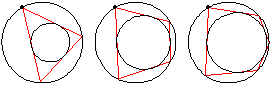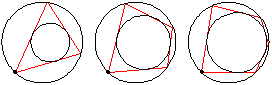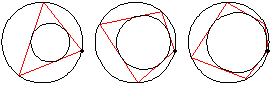
If an -sided
Poncelet transverse constructed for two given
conic sections is closed for one point of origin,
it is closed for any position of the point of origin. Specifically, given one ellipse inside another, if there exists one circuminscribed
(simultaneously inscribed in the outer and circumscribed on the inner)
-gon, then any point on the boundary of the outer ellipse
is the vertex of some circuminscribed
-gon. If the conic is taken as a circle (Casey 1888, pp. 124-126)
, then a polygon which has both an incenter and a circumcenter (and for which the
transversals would therefore close) is called a bicentric
polygon.
Amazingly, this problem is isomorphic to Gelfand's question (King 1994).
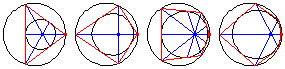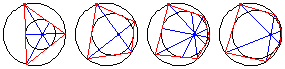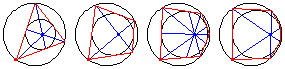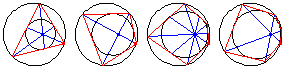
For an even-sided polygon, the diagonals are concurrent at the limiting point of the two circles, whereas for an odd-sided polygon, the lines connecting the vertices to the opposite points of tangency are concurrent at the limiting point.
Inverting about either of the two limit points gives two concentric circles. However, the -gonal sides become arcs of circles in the process, so this
sort of simple inversion does not provide an automatic
proof of the theorem (as happens in Steiner's porism,
for example).
Fuss (1792) derived formulas not only for the bicentric quadrilateral, but also the bicentric pentagon,
hexagon, heptagon, and octagon, as did Steiner (Fuss 1792; Jacobi 1823; Steiner
1827; Dörrie 1965, p. 192). Chaundy (1923) exhibited porisms for , 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18, 20, as well as erroneous
expressions for several other values (Kerawala 1947). Richelot derived the expression
for
.
In fact, there is a general analytic expression relating the circumradius
, inradius
, and offset between the circumcenter
and incenter
for a bicentric polygon. Given
,
, and
, define
|
(1)
| |||
|
(2)
| |||
|
(3)
|
Note that since ,
, and
are positive quantities with
,
.
Now let
 |
(4)
| ||
|
(5)
|
and define the elliptic modulus via
|
(6)
|
Then the condition for an -gon to be bicentric is
|
(7)
|
where
is a Jacobi elliptic function and
is a complete
elliptic integral of the first kind (Richelot 1830, Kerawala 1947). Kerawala
(1947) was able to establish many porisms in simple explicit form without resorting
to the use of elliptic functions.
For the two circles illustrated above, the tangent on the inner circle can be determined by solving
|
(8)
|
where
|
(9)
| |||
|
(10)
| |||
![[d+rcosphi; rsinphi],](/images/equations/PonceletsPorism/Inline45.svg) |
(11)
|
is the radius of the inner circle,
is the offset of the inner circle,
is the given position on the outer
circle, and
is the angle around the inner circle at which the tangent occurs. Taking the dot
product and simplifying gives
|
(12)
|
When this is solved for , the point at which the extension of this line intersects
the outer circle again can be found using the standard equation of a circle-line
intersection.
The degrees
of the algebraic equations relating
,
, and
for
, 4, ..., are 1, 2, 3, 4, 6, 8, 9, 12, 15, 16, 21, 24, 24,
32, 36, ... (OEIS A002348; Kerawala 1947).
Let the prime factorization of
be written as
|
(13)
|
then
in general is given by
|
(14)
|
In the following expressions, write
|
(15)
| |||
|
(16)
| |||
|
(17)
| |||
|
(18)
| |||
|
(19)
| |||
|
(20)
| |||
|
(21)
| |||
|
(22)
| |||
|
(23)
| |||
|
(24)
| |||
|
(25)
| |||
|
(26)
| |||
|
(27)
| |||
|
(28)
| |||
|
(29)
| |||
|
(30)
|
following Kerawala (1947), and
|
(31)
| |||
|
(32)
|
following Richelot (1830).
The equation for a bicentric triangle (), i.e., any triangle, may be variously written as
|
(33)
|
|
(34)
|
|
(35)
|
|
(36)
|
(Richelot 1830), or
|
(37)
|
(Steiner 1827; F. Gabriel-Marie 1912, pp. 497-501; Kerawala 1947; Altshiller-Court 1952, pp. 85-87; Wells 1992). The latter is sometimes known as the Euler triangle formula.
For a bicentric quadrilateral (), the radii and offset are connected by the equation
|
(38)
|
(Kerawala 1947), which expands to
|
(39)
|
(Davis; Durége; Casey 1888, pp. 109-110; F. Gabriel-Marie 1912, pp. 321 and 814-816; Johnson 1929; Dörie 1965). This can also be written
|
(40)
|
|
(41)
|
(Steiner 1827), or
|
(42)
|
(Richelot 1830).
The relationship for a bicentric pentagon () is
 |
(43)
|
(Steiner 1827) or
|
(44)
|
(Richelot 1830). A number of alternative forms are given by
|
(45)
|
|
(46)
|
|
(47)
|
 |
(48)
|
 |
(49)
|
and
|
(50)
|
(Kerawala 1947).
For ,
|
(51)
|
(Steiner 1827),
|
(52)
|
(Richelot 1830),
|
(53)
|
or
|
(54)
|
(Kerawala 1947).
For ,
|
(55)
|
(Jacobi 1823, Kerawala 1947)
For ,
|
(56)
|
(Kerawala 1947), which can also be written in the form
|
(57)
|
(Richelot 1830, Jacobi 1823). The equation given by Steiner (1827) contains (at least one) typographical error.
For ,
|
(58)
|
for ,
![16p^2q^2(p^2-1)(q^2-1)[p^4q^4-(p^2-q^2)^2]^2
={[p^4-(p^2q^2-q^2)^2]^2+[q^4-(p^2q^2-p^2)^2]^2+[p^4q^4-(p^2-q^2)^2]^2}^2](/images/equations/PonceletsPorism/NumberedEquation33.svg) |
(59)
|
(Richelot).
For ,
![64p^4q^4(p^2-1)(q^2-1)[p^4q^4-(p^2-q^2)^2]^2
={[p^4-(p^2q^2-q^2)^2]^2+[q^4-(p^2q^2-p^2)^2]^2+[p^4q^4-(p^2-q^2)^2]^2}^2](/images/equations/PonceletsPorism/NumberedEquation34.svg) |
(60)
|
(Richelot).
For ,
|
(61)
|
For ,
|
(62)
|
(Kerawala 1947) or
}^4
={[p^4-(p^2q^2-q^2)^2]^2+[q^4-(p^2q^2-p^2)^2]^2+[p^4q^4-(p^2-q^2)^2]^2}^4](/images/equations/PonceletsPorism/NumberedEquation37.svg) |
(63)
|
(Richelot 1830).
Weill (1878) gave an algorithm for finding approximate solutions for porisms with even
. The following table gives the approximate relations for fixed
.
| error | |||
| 6 | |||
| 8 | |||
| 10 |