The pentagonal icositetrahedron is the 24-faced dual polyhedron of the snub cube. It is illustrated above together with a wireframe version and a net that can be used for its construction.
The mineral cuprite () forms in pentagonal icositetrahedral crystals (Steinhaus
1999, pp. 207 and 209).
It is Wenninger dual .
Because it is the dual of the chiral snub cube, the pentagonal icositetrahedron also comes in two enantiomorphous forms, known as laevo (left) and dextro (right). An attractive dual of the two enantiomers superposed on one another is illustrated above.
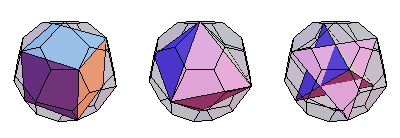
A cube, octahedron, and stella octangula can all be inscribed on the vertices of the pentagonal icositetrahedron (E. Weisstein, Dec. 25, 2009).
Surprisingly, the tribonacci constant
is intimately related to the metric properties of the pentagonal icositetrahedron
cube.
Its irregular pentagonal faces have vertex angles of
|
(1)
| |||
|
(2)
| |||
|
(3)
|
(four times) and
|
(4)
| |||
|
(5)
| |||
|
(6)
|
(once), where is a polynomial root
and
is the tribonacci constant.
The dual formed from a snub cube with unit edge length has side lengths
|
(7)
| |||
|
(8)
| |||
|
(9)
| |||
|
(10)
| |||
|
(11)
| |||
|
(12)
|
The circumradius is given by
|
(13)
| |||
 |
(14)
| ||
|
(15)
|
The surface area given by
|
(16)
| |||
 |
(17)
| ||
|
(18)
|
and volume given by
|
(19)
| |||
 |
(20)
| ||
|
(21)
|
