|
|
|
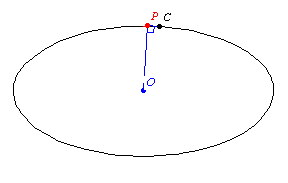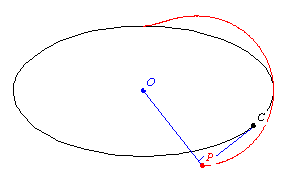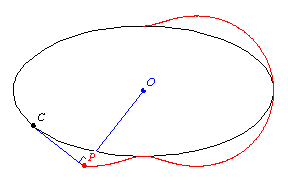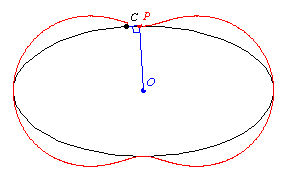
The pedal of a curve
with respect to a point
is the locus of the foot of the perpendicular
from
to the tangent
to the curve. More precisely, given a curve
, the pedal curve
of
with respect to a fixed point
(called the pedal point) is
the locus of the point
of intersection of the perpendicular from
to a tangent
to
. The parametric equations for a curve
relative to the pedal
point
are given by
|
(1)
| |||
|
(2)
|
If a curve
is the pedal curve of a curve
, then
is the negative pedal curve
of
(Lawrence 1972, pp. 47-48).
When a closed curve rolls on a straight line, the area between the line and roulette after a complete revolution by any point on the curve is twice the area of the pedal curve (taken with respect to the generating point) of the rolling curve.