The continued fraction for 
is [0; 1, 2, 3, 1, 6, 3, 1, 1, 2, 1, 1, 1, 1, 3, 10, ...]
(OEIS A016730). It has been computed to 
terms by E. Weisstein (Aug. 21, 2013).
The Engel expansion is 2, 3, 7, 9, 104, 510, 1413, ... (OEIS A059180).
The incrementally largest terms in the continued fraction are 0, 1, 2, 3, 6, 10, 13, 14, ... (OEIS A120754), which occur at positions 0, 1, 2, 3, 5, 15, 28, ... (OEIS A120755).
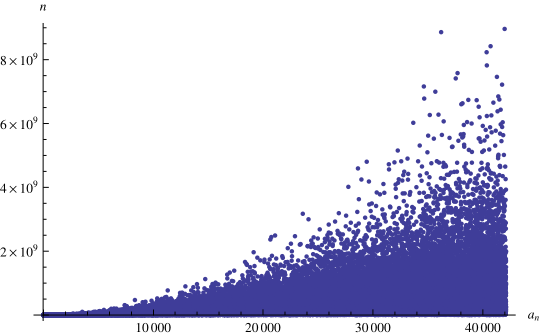
The plot above shows the positions of the first occurrences of 1, 2, 3, ... in the continued fraction, the first few of which are 1, 2, 3, 30, 40, 5, 29, 89, 88, 15,
... (OEIS A228269). The smallest number not
occurring in the first 
terms of the continued fraction are 42112, 42387,
43072, 45089, ... (E. Weisstein, Aug. 21, 2013).
Let the continued fraction of 
be denoted ![[a_0;a_1,a_2,...]](/images/equations/NaturalLogarithmof2ContinuedFraction/Inline5.svg)
and let the denominators of the convergents
be denoted 
, 
, ..., 
. Then plots above show successive values of 
, 
, 
, which appear to converge to Khinchin's
constant (left figure) and 
, which appear to converge to the Lévy
constant (right figure), although neither of these limits has been rigorously
established.
