The curve produced by fixed point on the circumference of
a small circle of radius
rolling around the inside of a large
circle of radius
. A hypocycloid is therefore a hypotrochoid
with
.
To derive the equations of the hypocycloid, call the angle by which a point on the small circle rotates about its
center ,
and the angle from the center of the large circle
to that of the small circle
. Then
|
(1)
|
so
|
(2)
|
Call . If
, then the first point is at minimum radius, and the
Cartesian parametric equations of the hypocycloid are
|
(3)
| |||
|
(4)
| |||
|
(5)
| |||
|
(6)
|
If instead so the first point is at
maximum radius (on the circle), then the equations of
the hypocycloid are
|
(7)
| |||
|
(8)
|
The curvature, arc length, and tangential angle of a hypocycloid are given by
|
(9)
| |||
|
(10)
| |||
|
(11)
|
An -cusped hypocycloid has
. For
an integer and with
, the equations of the hypocycloid therefore become
|
(12)
| |||
|
(13)
|
and the arc length and area are therefore
|
(14)
| |||
|
(15)
|
A 2-cusped hypocycloid is a line segment (Steinhaus 1999, p. 145; Kanas 2003), as can be seen by setting in equations (◇) and (◇) and noting that the
equations simplify to
|
(16)
| |||
|
(17)
|
This result was noted by the Persian astronomer and mathematician Nasir Al-Din al-Tusi (1201-1274), and is sometimes known as a "Tusi couple" is his honor (Sotiroudis and Paschos 1999, p. 60; Kanas 2003).
The following tables summarizes the names given to this and other hypocycloids with special integer values of .
| hypocycloid | |
| 2 | line segment (Tusi couple) |
| 3 | deltoid |
| 4 | astroid |
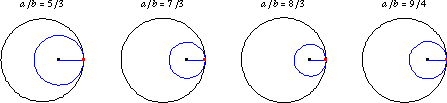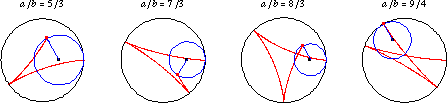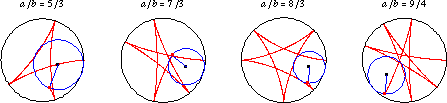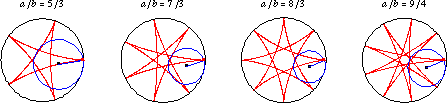
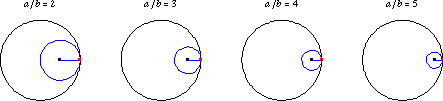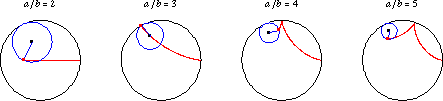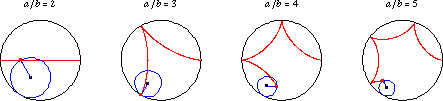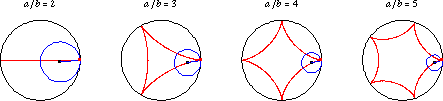
If is rational, then the curve eventually
closes on itself and has
cusps. Hypocycloids for a number of rational values
of
are illustrated above.
If is irrational,
then the curve never closes on itself. Hypocycloids for a number of irrational
values of
are illustrated above.
-cusped hypocycloids can also be constructed
by beginning with the diameter of a circle,
offsetting one end by a series of steps while at the same time offsetting the other
end by steps
times as large in the opposite direction and extending beyond the edge of the circle. After traveling around the circle
once, an
-cusped
hypocycloid is produced, as illustrated above (Madachy 1979).
Let be the radial distance from a fixed point.
For radius of torsion
and arc length
, a hypocycloid can given by the equation
|
(18)
|
(Kreyszig 1991, pp. 63-64). A hypocycloid also satisfies
|
(19)
|
where
|
(20)
|
and is the angle
between the radius vector and the tangent
to the curve.
The equation of the hypocycloid can be put in a form which is useful in the solution of calculus of variations problems with
radial symmetry. Consider the case , then
![r^2=x^2+y^2
=[(a-b)^2cos^2phi-2(a-b)bcosphicos((a-b)/bphi)+b^2cos^2((a-b)/bphi)+(a-b)^2sin^2phi+2(a-b)bsinphisin((a-b)/bphi)+b^2sin^2((a-b)/bphi)]
={(a-b)^2+b^2-2(a-b)b[cosphicos((a-b)/bphi)-sinphisin((a-b)/bphi)]}
=(a-b)^2+b^2-2(a-b)bcos(a/bphi).](/images/equations/Hypocycloid/NumberedEquation6.svg) |
(21)
|
But , so
, which gives
|
(22)
| |||
|
(23)
| |||
|
(24)
| |||
|
(25)
| |||
|
(26)
| |||
|
(27)
|
Now let
|
(28)
|
so
|
(29)
|
|
(30)
|
then
|
(31)
| |||
|
(32)
|
The polar angle is
 |
(33)
|
But
|
(34)
| |||
|
(35)
| |||
|
(36)
|
so
 |
(37)
| ||
 |
(38)
| ||
![(a[sin((a-rho)/aOmegat)+sin((a+rho)/aOmegat)]+rho[sin((a-rho)/aOmegat)-sin((a+rho)/aOmegat)])/(a[cos((a-rho)/aOmegat)-cos((a+rho)/aOmegat)]+rho[cos((a-rho)/aOmegat)+cos((a+rho)/aOmegat)])](/images/equations/Hypocycloid/Inline118.svg) |
(39)
| ||
 |
(40)
| ||
 |
(41)
|
Computing
![([atan(Omegat)-rhotan(rho/aOmegat)+tan(rho/aOmegat)][atan(Omegat)tan(rho/aOmegat)+rho])/([atan(Omegat)tan(rho/aOmegat)+rho]-[atan(Omegat)-rhotan(rho/aOmegat)]tan(rho/aOmegat))](/images/equations/Hypocycloid/Inline127.svg) |
(42)
| ||
![(atan(Omegat)[1+tan^2(rho/aOmegat)])/(rho[1+tan^2(rho/aOmegat)])](/images/equations/Hypocycloid/Inline130.svg) |
(43)
| ||
|
(44)
|
then gives
|
(45)
|
Finally, plugging back in gives
|
(46)
| |||
|
(47)
|
This form is useful in the solution of the sphere with tunnel problem, which is the generalization of the brachistochrone problem, to find the shape of a tunnel drilled through a sphere (with gravity varying according to Gauss's law) in a gravitational field such that the travel time between two points on the surface of the sphere under the force of gravity is minimized.