TOPICS
Search

Hyperbolic Cosecant

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
Csch
CschReIm
CschContours

The hyperbolic cosecant is defined as

cschz=1/(sinhz)=2/(e^z-e^(-z)).
(1)

It is implemented in the Wolfram Language as Csch[z].

It is related to the hyperbolic cotangent though

cschz=coth(1/2z)-cothz.
(2)

The derivative is given by

d/(dz)cschz=-cothzcschz,
(3)

where cothz is the hyperbolic cotangent, and the indefinite integral by

intcschzdz=ln[sinh(1/2z)]-ln[cosh(1/2z)]+C,
(4)

where C is a constant of integration.

It has Taylor series

cschz=sum_(n=-1)^(infty)(2^(n+1)B_(n+1)(1/2))/((n+1)!)z^n
(5)
=1/z-sum_(n=1)^(infty)(2(2^(2n-1)-1)B_(2n))/((2n)!)z^(2n-1)
(6)
=1/z-z/6+(7z^3)/(360)-(31z^5)/(15120)+...
(7)

(OEIS A036280 and A036281), where B_n(x) is a Bernoulli polynomial and B_n is a Bernoulli number.

Sums include

sum_(k=1)^(infty)csch^2(pik)=1/6-1/(2pi)
(8)
=0.007511723...
(9)

(OEIS A110191; Berndt 1977).

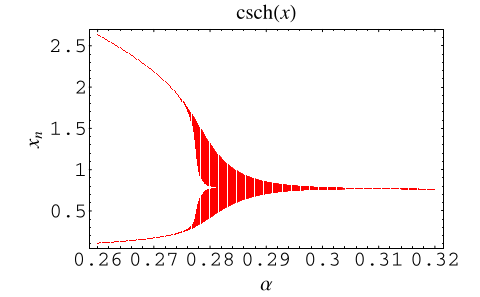
CschBifurcation

The plot above shows a bifurcation diagram for csch(x+alpha).

See also

Bernoulli Number, Bipolar Coordinates, Bipolar Cylindrical Coordinates, Cosecant, Helmholtz Differential Equation--Toroidal Coordinates, Hyperbolic Functions, Hyperbolic Sine, Inverse Hyperbolic Cosecant, Poinsot's Spirals, Surface of Revolution, Toroidal Function

Explore with Wolfram|Alpha

WolframAlpha

More things to try:

References

Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.Berndt, B. C. "Modular Transformations and Generalizations of Several Formulae of Ramanujan." Rocky Mtn. J. Math. 7, 147-189, 1977.Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.Sloane, N. J. A. Sequences A036280, A036281, and A110191 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. and Oldham, K. B. "The Hyperbolic Secant sech(x) and Cosecant csch(x) Functions." Ch. 29 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 273-278, 1987.Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.

Referenced on Wolfram|Alpha

Hyperbolic Cosecant

Cite this as:

Weisstein, Eric W. "Hyperbolic Cosecant." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/HyperbolicCosecant.html

Subject classifications