There are three theorems related to pedal circles that go under the collective title of the Fontené theorems.
The first Fontené theorem lets be a triangle and
an arbitrary point,
be the medial
triangle of
,
and
be the pedal triangle of
with respect to
. Denote the intersections of the corresponding sides of
and
as
,
, and
(e.g.,
is the intersection of
and
, etc.), then the lines
,
and
meet at a point
common to the circumcircles of
(which is the nine-point
circle of
)
and
(which is the pedal circle of
with respect to
).
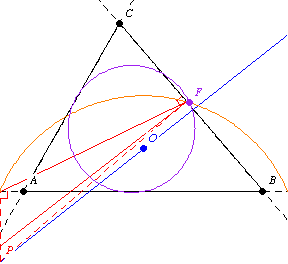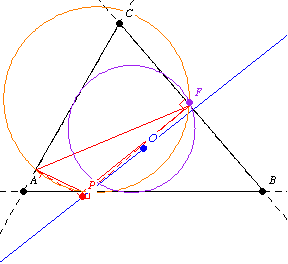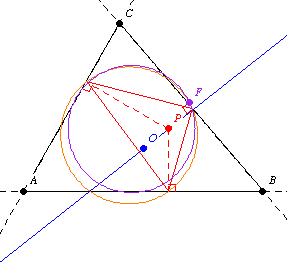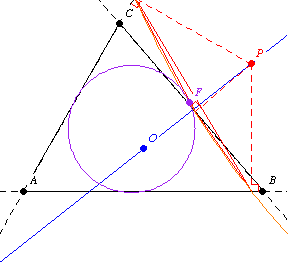
The second Fontené theorem states that if a point moves on a fixed line through the circumcenter, then its pedal circle passes through a fixed point on the nine-point circle, as illustrated above.
The third Fontené theorem states that the pedal circle of a point
is tangent to the nine-point circle iff
and its isogonal
conjugate
lie on a line through the circumcenter.
(Note that Johnson (1929) erroneously states this theorem with the orthocenter
in place of the circumcenter.) Feuerbach's
theorem is a special case of this theorem.