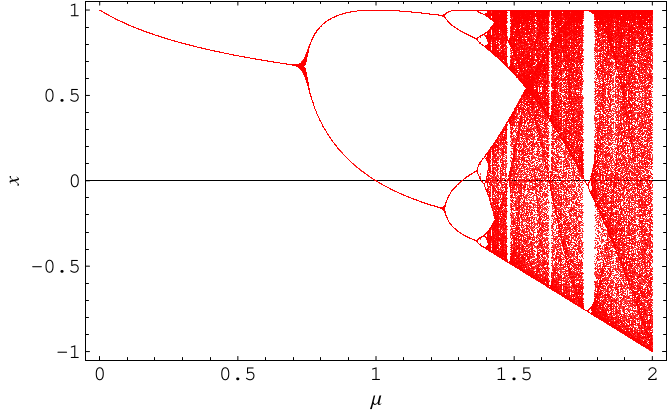
The Feigenbaum constant is a universal constant for functions approaching chaos
via period doubling. It was discovered by Feigenbaum
in 1975 (Feigenbaum 1979) while studying the fixed points of the iterated function
|
(1)
|
and characterizes the geometric approach of the bifurcation parameter to its limiting value as the parameter is increased for fixed
. The plot above is made by iterating equation (1)
with
several hundred times for a series of discrete but closely spaced values of
, discarding the first hundred or so
points before the iteration has settled down to its fixed points, and then plotting
the points remaining.
A similar plot that more directly shows the cycle may be constructed by plotting
as a function of
.
The plot above (Trott, pers. comm.) shows the resulting curves for
, 2, and 4.
Let
be the point at which a period
-cycle appears, and denote the converged value by
. Assuming geometric convergence, the difference between
this value and
is denoted
|
(2)
|
where
is a constant and
is a constant now known as the Feigenbaum constant. Solving for
gives
|
(3)
|
(Rasband 1990, p. 23; Briggs 1991). An additional constant , defined as the separation of adjacent elements of period doubled attractors
from one double to the next, has a value
|
(4)
|
where
is the value of the nearest cycle element to 0 in the
cycle (Rasband 1990, p. 37; Briggs 1991).
For equation (1) with , the onsets of bifurcations occur at
, 1.25, 1.368099, 1.39405, 1.399631, ..., giving convergents
to
for
,
2, 3, ... of 4.23374, 4.5515, 4.64617, ....
For the logistic map,
|
(5)
| |||
|
(6)
| |||
|
(7)
| |||
|
(8)
|
(OEIS A006890, A098587, and A006891; Broadhurst 1999; Wolfram 2002,
p. 920),
where
is known as the Feigenbaum constant and
is the associated "reduction parameter."
Briggs (1991) calculated to 84 digits, Briggs (1997) to 576 decimal places (of
which 344 were correct), and Broadhurst (1999) to 1018 decimal places. It is not
known if the Feigenbaum constant
is algebraic, or if it can be expressed in terms of other
mathematical constants (Borwein and Bailey 2003, p. 53).
Briggs (1991) calculated to 107 digits, Briggs (1997) to 576 decimal places (of
which 346 were correct), and Broadhurst (1999) to 1018 decimal places.
Amazingly, the Feigenbaum constant and associated reduction parameter
are "universal" for all one-dimensional maps
if
has a single locally quadratic maximum.
This was conjecture by Feigenbaum, and demonstrated rigorously by Lanford (1982)
for the case
,
and by Epstein (1985) for all
.
More specifically, the Feigenbaum constant is universal for one-dimensional maps if the Schwarzian derivative
|
(9)
|
is negative in the bounded interval (Tabor 1989, p. 220). Examples of maps which are universal include the Hénon
map, logistic map, Lorenz
attractor, Navier-Stokes truncations, and sine map . The value of the Feigenbaum constant can
be computed explicitly using functional group renormalization theory. The universal
constant also occurs in phase transitions in physics.
The value of
for a universal map may be approximated from functional group renormalization theory
to the zeroth order by solving
![1-alpha^(-1)=(1-alpha^(-2))/([1-alpha^(-2)(1-alpha^(-1))]^2),](/images/equations/FeigenbaumConstant/NumberedEquation6.svg) |
(10)
|
which can be rewritten as the quintic equation
|
(11)
|
Solving numerically for the smallest real root gives , only 0.7% off from the actual value (Feigenbaum
1988).
For an area-preserving two-dimensional map with
|
(12)
| |||
|
(13)
|
the Feigenbaum constant is (Tabor 1989, p. 225).
For a function of the form (1), the Feigenbaum constant for various
is given in the following table (Briggs 1991, Briggs et al. 1991, Finch 2003),
which updates the values in Tabor (1989, p. 225).
| 3 | 5.9679687038... | 1.9276909638... |
| 4 | 7.2846862171... | 1.6903029714... |
| 5 | 8.3494991320... | 1.5557712501... |
| 6 | 9.2962468327... | 1.4677424503... |
Broadhurst (1999) considered additional Feigenbaum constants. Let and
be even functions with
and
|
(14)
| |||
|
(15)
|
and
as large as possible. Let
be positive numbers with
|
(16)
|
and
as small as possible. Also let
be the order of the nearest singularity, with
|
(17)
|
as
tends to zero. The values of these constants are summarized in the following table.