A class of complete orientable minimal surfaces of derived from Enneper's
minimal surface. They are named for the mathematicians who found the first two
examples in 1982.
The Chen-Gackstatter surfaces form a double-indexed collection , where
and
.
is Enneper's
minimal surface, and
is obtained from
by adding
handles so that it has topological genus equal to
. It has one Enneper end with winding order three, meaning
that, like Enneper's minimal surface,
it has a symmetric three-fold shape which tends to coincide with a triple plane far
away from the center.
In general,
has total curvature
, topological genus
, and one Enneper end of winding order
. This property distinguishes it from other surfaces such
as the catenoid which have two ends of winding order
1.
The first Chen-Gackstatter surface has topological genus
and total curvature
. Its Enneper-Weierstrass
parameterization is given by
|
(1)
| |||
|
(2)
|
where
is the Weierstrass elliptic function
with parameters
 |
(3)
| ||
|
(4)
|
with
the imaginary unit (and where
turns out to be real and positive), and the constant
given by
 |
(5)
|
López (1992) has shown that is the only genus one orientable complete minimal surface
of total curvature
.
In a neighborhood of the origin can be approximated by the following parametric equations:
|
(6)
| |||
|
(7)
| |||
|
(8)
|
where
is a small positive constant and
.
The second Chen-Gackstatter surface has topological genus
and total curvature
. Its Enneper-Weierstrass
parameterization is
 |
(9)
| ||
 |
(10)
|
where ,
,
and
are positive numbers such that
and, given the definitions
 |
(11)
| ||
 |
(12)
| ||
 |
(13)
| ||
 |
(14)
|
it holds that
|
(15)
|
and
|
(16)
|
The surfaces
and
were classified by Karcher (1989) and Thayer (1995), respectively. Sato (1996) completed
the work for all
, and proved that the Enneper-Weierstrass parameterization
of
is given by
|
(17)
| |||
|
(18)
|
where
 |
(19)
|
and ,
are suitable real numbers. They can be chosen in such a way that the triple
|
(20)
|
does not depend on the value of .
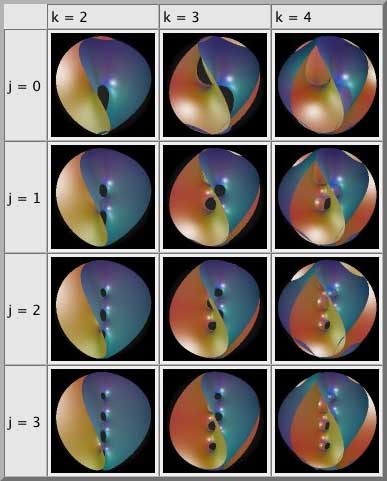
The pictures above (Hoffman et al. ) visualize the role of the double-index:
has
holes along its axis of symmetry, which is surrounded by a curly rim with
mountains and valleys.