A
function is a function that is differentiable
for all degrees of differentiation. For instance,
(left figure above) is
because its
th derivative
exists and is continuous.
All polynomials are
.
The reason for the notation is that C-k
have
continuous derivatives.
functions are also called "smooth" because neither they nor their derivatives
have "corners," which would make their graph look somewhat rough. For example,
is not smooth (right figure above).
There are special
functions which are very useful in analysis and geometry. For example, there are
smooth functions called bump functions, which are
smooth approximations to a characteristic
function. Typically, these functions require some calculus
to show that they are indeed
.
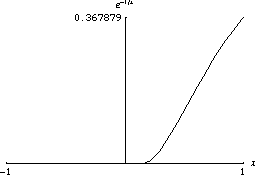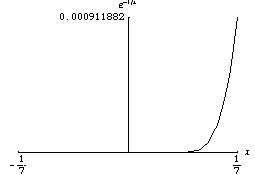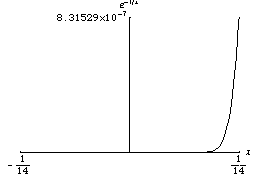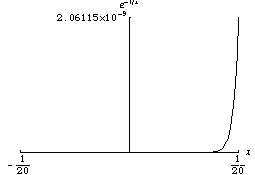
Any analytic function is smooth. But a smooth function is not necessarily analytic. For instance, an analytic function cannot be a bump function. Consider the following function, whose Taylor series at 0 is identically zero, yet the function is not zero:
 |
(1)
|
The function
goes to zero very quickly. One property of smooth functions is that they can look
very different at different scales.
The set of smooth functions cannot be made into a Banach space, which makes some problems hard, but instead has the weaker structure of a Fréchet space.