Given any open set in
with compact closure
, there exist smooth functions
which are identically one on
and vanish arbitrarily close to
. One way to express this more precisely is that for any open set
containing
, there is a smooth function
such that
1. for all
and
2. for all
.
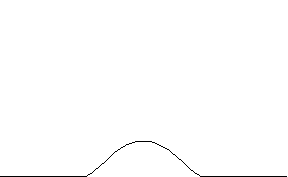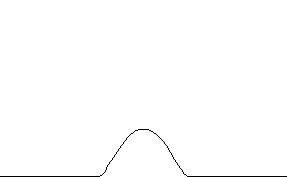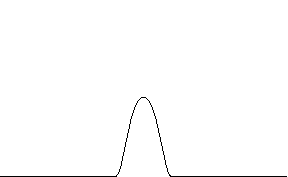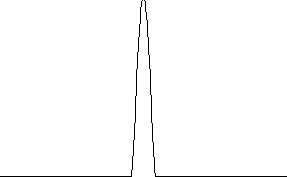
A function
that satisfies (1) and (2) is called a bump function. If
then by rescaling
, namely
, one gets a sequence of smooth functions which
converges to the delta function, providing that
is a neighborhood of 0.